Storia del logaritmo

Il concetto di logaritmo è molto antico. Sia i Babilonesi che gli Egizi studiarono problemi legati alla vita quotidiana che utilizzano progressioni aritmetiche e geometriche e, anche se non costruirono teorie, nei loro documenti sono state individuate alcune idee che portarono molto più tardi alla nascita del concetto di logaritmo.

È stata ritrovata una tavoletta babilonese, risalente al 2000 a.C. circa, su cui si legge il seguente problema: "Un capitale di una mina, posto all'interesse del 20% dopo 5 anni raddoppia; se il capitale così raddoppiato si mette a frutto e dopo 5 anni si reinveste tutto il capitale raddoppiato e così via..., quale sarà il capitale accumulato dopo 6 lustri?" (un lustro = 5 anni; la mina era una moneta in uso presso i Babilonesi). 

Nel Papiro di Rhind, un importante documento della matematica Egizia, scritto intorno al 1650 a.C. e contenente una raccolta di calcoli, tabelle e problemi con le relative soluzioni, si legge il seguente problema: "Se ti dicono: si hanno 10 misure di grano distribuito tra 10 persone in modo che la differenza tra ciascuna persona e la successiva, in grano, sia 1/8, fai così: prendi la misura intermedia e chiamala 1, fai la metà della differenza, cioè 1/16, prendi questa nove volte, ottieni 1/2+1/16, aggiungi a questo la razione intermedia"

In Grecia Pitagora (circa 540 a.C.) utilizzò le progressioni nei numeri figurati (numeri interi che possono essere rappresentati mediante uno schema geometrico regolare, nel piano o nello spazio), Euclide (circa 300 a.C.) parlò delle progressioni a proposito dei numeri perfetti (numeri uguali alla somma dei suoi divisori propri, cioè tutti tranne se stesso, 1 incluso. La successione dei numeri perfetti comincia con 1, 6, 28, 496, 8.128).

Archimede di Siracusa (287?-212 a.C.) esamina la “legge degli esponenti” nella sua opera "Arenario", opera molto importante per la storia della matematica e dell’astronomia.

La “legge degli esponenti” si basa sull’osservazione della relazione che esiste tra le progressioni aritmetiche e geometriche; infatti se a_n=a₀.qⁿ e a_m=a₀.q^m sono due termini di una progressione geometrica, il loro prodotto occupa la posizione n+m nella progressione, quindi al prodotto tra i due termini a_n e a_m corrisponde una somma, ovvero ad una progressione geometrica ne corrisponde una aritmetica.  

Se, ad esempio, si considerano i primi 10 termini della progressione geometrica di ragione 3 e si riportano in una tabella con a fianco indicato il posto (indice) occupato da ogni termine, si ha:

Si può osservare che moltiplicando tra loro due termini qualsiasi della progressione si ottiene ancora un termine della progressione, il cui indice è dato dalla somma degli indici dei due fattori; moltiplicando ad esempio 9^.243=2187=a₇ e sommando gli indici corrispondenti, che sono 2 e 5, si ottiene 7 che è l’indice del termine 2187, da cui oggi 9=3², 243=3⁵ e 9^.243=3^2. 3⁵=3²⁺⁵=3²⁺⁵=2187.

Non avendo a disposizioni calcolatrici o computer, ridurre prodotti in somme, semplifica i calcoli e questa proprietà è il motivo della grande importanza dei logaritmi. Analogamente si può ridurre una divisione a una sottrazione e una potenza a una moltiplicazione.

Nel XV sec. il matematico Chuquet studia la progressione aritmetica di ragione 1 e la progressione geometrica di ragione 2:

Enuncia poi questa regola:
"Chi moltiplica uno di questi termini della progressione geometrica per un altro e somma i due ordini nei quali sono situati i due numeri moltiplicati, trova il posto dove deve essere situato il risultato della moltiplicazione."

Anche Chuquet non giunse, però, ad esprimere i termini della progressione geometrica sotto forma di potenza e ciò fu un limite per i suoi risultati. Si avvicina però al concetto di funzione logaritmica riflettendo su un problema detto il problema della botte: "Una botte si vuota ogni giorno di un decimo del suo contenuto; dopo quanto sarà vuota a metà?"

La soluzione di Chuquet utilizza gli strumenti del tempo (che saranno descritti in seguito) ed è perciò solo approssimata.

Il matematico Stifel nel libro Aritmetica Integra (1544) estende le relazioni tra progressione aritmetica e progressione geometrica parlando anche di esponenti negativi.

Riprendendo l'idea di Chuquet, fa notare che, anche usando questa tabella contenente frazioni e numeri relativi, la moltiplicazione tra due valori può essere sostituita dall'addizione algebrica tra termini corrispondenti, mentre la divisione può essere sostituita dalla sottrazione e così via.

Per esempio per calcolare il prodotto 1/8^_.16 si cercano le posizioni dei fattori. La posizione del prodotto è in corrispondenza della somma delle posizioni dei fattori -3+4=1; si cerca quindi il valore corrispondente a “+1” ossia 2.

La “legge” esposta non è però sempre valida, infatti ad esempio per il calcolo del prodotto 6^.12 non è utilizzabile in quanto i fattori 6 e 12 non sono termini della progressione geometrica. In questo caso si possono tuttavia utilizzare metodi che permettano di dare valori approssimati del prodotto. Tra questi l’interpolazione lineare, metodo che considera ogni numero come appartenente ad uno degli intervalli determinati dai valori della progressione e suppone che all'interno dell'intervallo valga la legge di proporzionalità. Tale algoritmo era in uso presso gli antichi egizi ed è fortemente legato al metodo della falsa posizione che sarà descritto  in seguito.

Ad esempio per determinare il valore approssimato del prodotto 6·12, si considerano rispettivamente gli intervalli (4;8) e (8;16) ai quali appartengono i due fattori e si osserva che 6 è il valor medio di 4 e 8 e 12 è il valor medio di 8 e 16 quindi si possono considerare i corrispondenti valori medi nella prima riga, in modo tale da far corrispondere a 6 il numero 2,5 (valore medio tra 2 e 3) e a 12 il numero 3,5 (valore medio tra 3 e 4). La somma dei valori corrispondenti 2,5 + 3,5 =6 in corrispondenza del quale si trova il valore 64.

Calcolato nel seguente modo il prodotto 6·12 risulterebbe 64, cioè un valore lontano dal vero valore 72 con l’errore causato dal supporre che esista proporzionalità fra le variazioni dei valori.  Il metodo è valido, l’errore “grande” deriva dal fatto che i numeri della progressione geometrica sono molto distanziati tra loro. Basterà quindi infittire i valori della progressione.

Ad esempio se si utilizza la progressione geometrica di ragione 1,1 si ha

Applicando il metodo di interpolazione lineare il fattore 6 è compreso tra i termini 5,6 e 6,1 ai posti 18 e 19 della successione. Si imposta la proporzione:

(19 - 18):(18+p - 18) = (6,1 – 5,6):(6 - 5,6) da cui p = 0,8. Allora la posizione corrispondente a 6 è 18 + 0,8 =18,8.

Analogamente per il fattore 12:

(27 - 26):(26+p - 26) = (13,1 – 11,9):(12 - 11,9) da cui p = 0,08. Allora la posizione corrispondente a 12 è 26 + 0,08 =26,08.

Si sommano le posizioni: 18,8+26,08=44,88, compresa tra 44 e 45 i cui valori corrispondenti nella progressione sono 66,3 e 72,9.

Allora 

(45-44):(44,88-44)=(72,9-66,3):(66,3+p-66,3) da cui p=5,8. Allora il valore approssimato del prodotto è 66,3+5,8=72,1.

Il matematico che ebbe il merito di introdurre i logaritmi fu John Napier (o Giovanni Nepero) (Merchiston Castle, 1550 – Edimburgo, 4 aprile 1617), che lavorò alla sua invenzione per vent’anni, prima di pubblicarne i risultati.  Egli, nelle sue opere, “Mirifici logarithmorum canonis descriptio” e “Mirifici logarithmorum constructio”, osservò che, per poter applicare la “legge degli esponenti” a qualsiasi prodotto di due numeri è necessario che i termini della successione geometrica siano molto vicini tra loro e scoprì che ciò si può ottenere utilizzando come ragione della progressione un numero molto vicino ad 1. Napier, decise di assumere a₀=10⁷ e ragione 1-10^-7 molto vicina a 1. Costruisce la progressione

La scelta della ragione non è casuale in quanto consente di facilitare il calcolo dei termini: il termine a_n si ottiene sottraendo ad a_n−1 il numero ottenuto spostando la virgola decimale di quest’ultimo di sette posti (a_n=a_n-1 - a_n-1^.10^-7). Quindi per sottrazioni successive Nepero calcolò (1-10^-7)ⁿ per n da 1 a 100 e 10⁷(1-10^-7)ⁿ con n da 1 a 50. Questi calcoli gli permisero di trovare per ogni numero intero N da 5 a 10 milioni il numero L che risolve l’equazione

 e chiamò L logaritmo di N.

Quindi ha calcolato quello che oggi indicheremmo con  

Osservando che

In questo modo quindi Nepero ha ottenuto un sistema di logaritmi che a parte il segno e la posizione della virgola decimale (fattore 10⁷), equivale a quelli che oggi vengono detti logaritmi naturali. In tale sistema

La corrispondenza con la definizione di logaritmo da noi utilizzata sta nel fatto che l’indice del termine non è altro che l’esponente da attribuire alla base prefissata per ottenere una potenza uguale al termine dato.

Inizialmente Nepero aveva chiamato i suoi indici di potenze “numeri artificiali”, più tardi introdusse il termine composto dalle due parole greche logos (ragione o rapporto) e arithmos (numero) e non aveva introdotto il concetto di base per il suo sistema.

Una differenza tra i logaritmi di Nepero e quelli utilizzati adesso sta nel fatto che la somma di due logaritmi neperiani era uguale al logaritmo di (N₁^.N₂)/10⁷ e non di N₁^.N₂. Analoga situazione si ripete per i quozienti e le potenze.

Nepero aveva spiegato i logaritmi, ossia quanto esposto precedentemente, anche con una definizione cinematica che poggia su due moti, il primo dei quali uniforme, detto a crescita aritmetica, il secondo, non uniforme, detto a crescita geometrica. Nella Constructio, Nepero definisce i due moti: crescere in modo aritmetico significa aumentare della stessa quantità in tempi uguali. Decrescere in modo geometrico significa diminuire in tempi uguali di una parte sempre proporzionale, dapprima a tutta la quantità e in seguito alle parti via via rimanenti.

Nepero prende in considerazione un punto che si muove su una semiretta di moto aritmetico ed un secondo punto che si muove su una semiretta di moto geometrico. Il segmento individuato sulla prima semiretta viene chiamato Logaritmo del secondo.

Egli considera G e A mobili su due rette parallele. Il mobile G si trova all’istante iniziale t = 0 in un punto T di un segmento TS di lunghezza 10⁷. All’istante t=0 G è animato da velocità v₀. Il moto di G è geometrico per cui si svolge con velocità istantanea proporzionale alla distanza di G dall’estremo S. Il punto A all’istante t = 0 si trova in B con la stessa velocità v₀ di G, ma il suo moto successivo è aritmetico, cioè uniforme. Detto C il punto raggiunto da A quando G si trova in D, allora Nepero definisce BC come il logaritmo di DS.

BC=logaritmo(DS)

Si osservi che da questa definizione di logaritmo segue che il logaritmo di TS è 0 dal momento che quando G è in T il punto C è in B e dunque AB=0.

Il sistema di logaritmi introdotto da Nepero fu accolto da un altro matematico Henry Briggs (1561-1639), che a seguito di una discussione con lo stesso Nepero, sulla possibilità di modificare il metodo dei logaritmi, introdusse, per semplificare i calcoli, l’utilizzo di potenze del dieci. I due matematici giunsero così alla conclusione che il logaritmo di uno fosse zero e il logaritmo di dieci fosse uno.

Briggs compilò la prima tavola dei logaritmi comuni o briggsiani e invece di prendere le potenze di un numero vicino ad uno, come aveva fatto Nepero, considerò come primo valore log10=1 e calcolò poi altri logaritmi mediante successive estrazioni di radici. Per esempio, considerando:

Le tavole logaritmiche utilizzate fino a pochi decenni fa sono tutte derivate da quelle di Briggs, il cui nome è rimasto associato ai logaritmi a base 10. Anche Briggs non diede però la definizione di logaritmo perché all’inizio del XVII secolo gli esponenti frazionari ed irrazionali non erano ancora in uso. 

Fu Eulero (1707-1783) a enunciare la definizione di logaritmo che ancora oggi viene utilizzata, ad applicarla in diversi campi della matematica e a considerare le funzioni esponenziali e logaritmiche che hanno come base il numero irrazionale 2,71828…, che oggi, sebbene sia chiamato impropriamente numero di Nepero, viene indicato con la lettera “e”, iniziale di Eulero. Questo numero, già presentato nel capitolo dei numeri irrazionali, è il limite della successione delle basi sempre più adatte ad applicare la legge degli esponenti:

Anche se Nepero fu il primo a pubblicare un’opera sui logaritmi, un altro matematico, Jobst Burgi (1552-1632), aveva sviluppato qualche anno prima delle idee simili a quelle di Nepero. Entrambi si erano basati su serie aritmetiche e geometriche; le differenze tra i due erano da attribuirsi alla terminologia utilizzata e a numeri utilizzati come base. Mentre Nepero utilizzò basi minori di uno, 1-10^-7, Burgi scelse un numero leggermente maggiore di uno, 1+10^-4 e invece di moltiplicare le potenze di questo numero per 10⁷, le moltiplicò per 10⁸.

Algoritmi per il calcolo approssimato di logaritmi

Teorema degli zeri

Se  è una funzione continua in un intervallo chiuso e limitato [a;b] e negli estremi di tale intervallo la funzione assume valori di segno opposto, f(a)^.f(b)<0 allora esiste almeno un punto x₀, interno all’intervallo (a,b), in cui la funzione si annulla, cioè f(x₀)=0.

Il teorema degli zeri è importante perché permette di risolvere equazioni, non risolvibili algebricamente, che si presentano nella forma f(x)=0, con f(x) funzione continua. Con esso si può stabilire se l'equazione ammette soluzioni ed in caso affermativo di localizzarli mediante metodi grafici, come il metodo di bisezione e della falsa posizione.

Metodo della falsa posizione

Il metodo della falsa posizione è un metodo per la risoluzione di problemi riconducibili ad equazioni o sistemi di equazioni lineari. I primi esempi di risoluzione di tali problemi (raccolti numerosi nel Papiro Rhind) riguardano l’equivalente della risoluzione di “equazioni di primo grado”. 

Esempio egizio

"Se sommiamo ad una quantità la sua settima parte, otteniamo 19. Quant’è la quantità?"

In notazione moderna il problema è equivalente alla risoluzione dell’equazione

Il metodo di risoluzione egizio, denominato di falsa posizione, consiste nell’attribuire all’incognita a primo membro il valore iniziale 7, determinando come valore conseguente a secondo membro il valore

L’argomentazione procede ipotizzando che se un certo "multiplo" di 8 dà 19, allora lo stesso multiplo" di 7 darà il numero richiesto.

La soluzione del problema si potrà quindi determinare risolvendo la proporzione 8:19=7:x, da cui 

Seppure la maggioranza dei problemi egizi corrisponde ad equazioni lineari, non mancano esempi di risoluzione di equazioni non lineari di secondo grado. Si tratta anche qui di casi particolari. Il Papiro di Berlino propone un sistema di secondo grado in due incognite. Ancora una volta la capacità aritmetica e la conoscenza di metodi risolutivi permettono di determinare le soluzioni; la strada è quella della falsa posizione. Come per matematiche future, gli Egiziani arrivano facilmente a problemi di secondo grado: dalle misure, o lunghezze, si passa a doppie misure e superfici.

Descrizione del metodo

Data una funzione f(x) continua in un intervallo chiuso [a, b] e tale che f(a)^.f(b)<0, con la radice (o zero della funzione) appartenente a tale intervallo

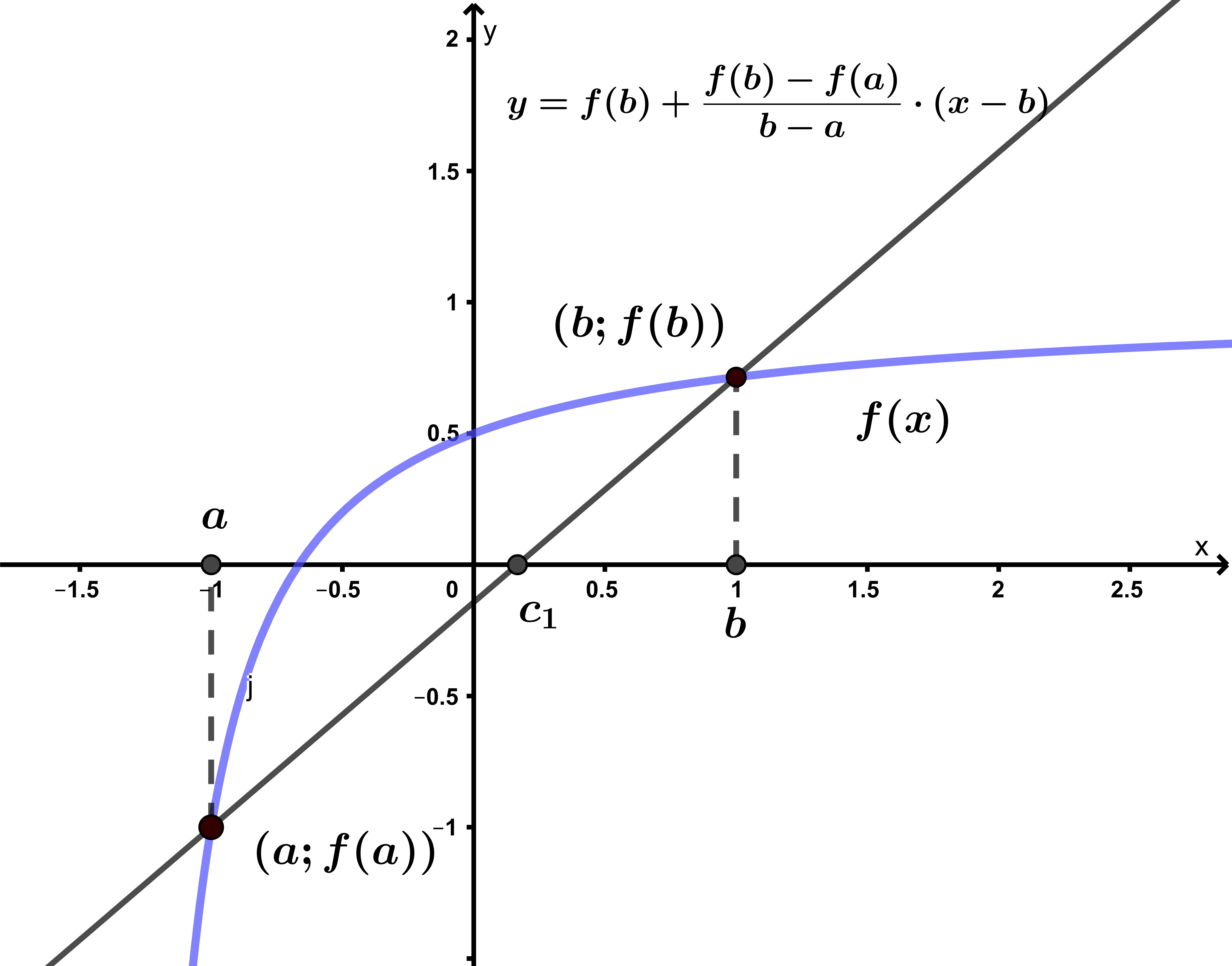
si determina l’equazione della retta passante per i punti (a, f(a)) e (b, f(b))

e si calcola il punto di intersezione della retta con l’asse delle ascisse, ponendo y =0

Si verifica l’appartenenza della radice α ad uno dei due intervalli [a, c₁] e [c₁, b] e si ripete la procedura, come nel caso del metodo delle bisezioni che vedremo in seguito, ponendo

                   

ad un generico passo k si ha:

e si pone:

Anche per questo metodo è possibile dimostrare la convergenza nella sola ipotesi di continuità della funzione f(x).

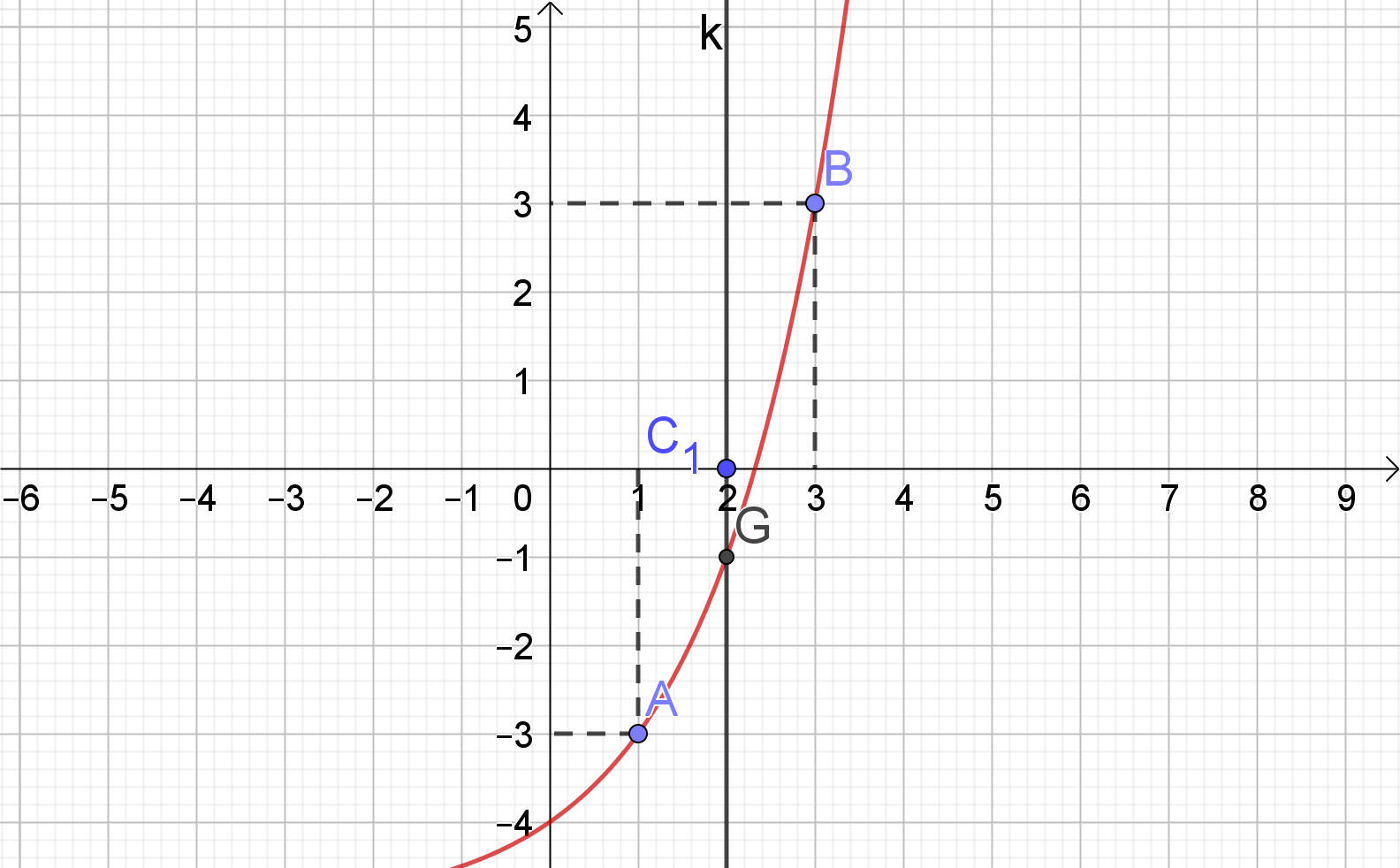
Ad esempio si determini il valore approssimato di log₂5 cioè della soluzione dell’equazione esponenziale 2^x=5

Bisogna quindi determinare gli zeri della funzione definita e continua in tutto l’insieme dei numeri reali f(x)=2^x-5         

Essendo 5 compreso tra 4 e 8 allora x risulta compreso tra 2 e 3.

Si ha f(2)=4-5=-1 e f(3)=8-5=3

Quindi si determina l’equazione della retta passante per i punti A(3,3) e B(2, -1)

L’ascissa del punto di intersezione della retta con l’asse x è

Quindi il valore approssimato di log₂5 al primo passo dell’algoritmo è 2,25.

 

Si determina l’ordinata del punto della funzione di ascissa 2,25

La retta passante per B₁=(2,25;-0.24317154) ha equazione y=4,32x-9,97 e interseca l’asse x nel punto di ascissa (approssimata) 2,31.

Quindi il valore approssimato di log₂5 al secondo passo dell’algoritmo è 2,31.

Il valore dato dalla calcolatrice è 2,3219280948873623478703194294894.

Il metodo di bisezione

Il metodo di bisezione (o algoritmo dicotomico) è il metodo numerico più semplice per trovare le soluzioni di una equazione f(x)=0 con f(x) definita e continua.

Si determinano due elementi a e b del dominio che abbiano immagini discordi f (a)⋅f(b)<0 . Si determina il punto medio dell’intervallo [a,b] e si calcola il valore della funzione nel punto.  Se l’immagine del punto medio è nulla allora si è trovata la soluzione esatta dell’equazione, altrimenti tra i due intervalli  

si sceglie quello ai cui estremi la funzione assume valori discordi. Si ripete per questo intervallo il procedimento di dimezzamento. Così continuando si ottiene una successione di intervalli ognuno incluso nel precedente con ampiezze decrescenti che contengono la soluzione.

Esempi

Si consideri ancora l’equazione 2^x=5 la cui soluzione abbiamo visto prima essere compresa tra 2 e 3.

f(2)=4-5=-1<0

f(3)=8-5=3>0

 

Quindi 2,25<log₂5<2,375

Per trovare le soluzioni di un'equazione f(x)=h(x)-g(x)=0 con f(x) continua inserire le equazioni delle funzioni h(g) e g(x)