La matematica finanziaria è quella parte della matematica che si occupa di problemi economico-finanziari, cioè di quei problemi aventi per oggetto capitali monetari. Essa in pratica applica gli strumenti della matematica al mondo della finanza e dell’economia. Il suo campo di applicazione si è considerevolmente ampliato nel corso del tempo: dall’occuparsi semplicemente delle operazioni di credito tra privati e con le banche, oggi si interessa anche di problemi dei mercati finanziari.

Poiché l'ammontare di un capitale non rimane costante al passare del tempo, il problema fondamentale della matematica finanziaria è confrontare tra loro capitali che si rendono disponibili a scadenze diverse. 

Distinguiamo le due seguenti operazioni finanziarie:

• capitalizzazione:  il trasferimento di denaro in avanti nel tempo (ad esempio un investimento di un capitale per un certo periodo di tempo)

• attualizzazione: '"inverso" della capitalizzazione, ed è l'operazione che consente di trasferire del denaro indietro nel tempo (ad esempio un prestito, ossia l'anticipo ad oggi una somma )

Soggetti Coinvolti

Nelle operazioni finanziarie agiscono 3 soggetti:

• chi dispone del capitale (parte);
• intermediari;
• chi richiede ed accetta il capitale (controparte).

Grandezze in gioco

Si definiscono le seguenti grandezze:

per la capitalizzazione

• C = capitale investito per avere il rendimento
• I = interesse fruttato da un capitale dopo un certo tempo
• M = montante: il capitale più l’interesse da questi fruttato in un certo periodo
• i = tasso di interesse applicato quando si capitalizza, cioè quando si calcolano gli interessi
• t = tempo del periodo d’investimento
• r = fattore di capitalizzazione (o di montante), funzione che esprime il montante di un capitale unitario in funzione del tempo

per l'attualizzazione

• V = valore attuale di una somma disponibile a scadenza
• D = sconto: l’importo da sottrarre ad una somma disponibile a scadenza per ottenere il suo valore attuale
• S = somma a scadenza da attualizzare
• d = tasso di sconto applicato quando si attualizza, cioè quando si sconta
• t = tempo 
• v = fattore di attualizzazione (o di sconto) funzione che esprime il valore attuale di un capitale unitario in funzione del tempo

I tre regimi finanziari

Il calcolo degli interessi non è univoco, ma dipende dal tipo di metodo (si dice “legge” o “regime” finanziario) che si vuole applicare e ci sono tre i metodi con cui calcolare gli interessi su un capitale:

• regime dell’interesse semplice (e dello sconto razionale)
• regime dello sconto commerciale
• regime dell’interesse composto (che è quello più utilizzato per le sue specifiche caratteristiche)

L’interesse semplice

In questo regime finanziario gli interessi sono direttamente proporzionali al capitale ed al tempo di investimento: proprio per tale caratteristica si dice che il regime dell’interesse semplice è una funzione lineare del tempo, secondo la proporzione
100∶ (i∙t) =C ∶ I da cui 

 ovvero, mantenendo i in percentuale,

Pertanto, sapendo che M = C + I, la formula per calcolare il montante è 

M = C + I = C + C ∙t∙ i = C (1 + i∙ t), ovvero

dove i è il tasso nell’unità di tempo espresso in forma decimale (per es. 0,035 per dire il 3,5%) e t è il tempo nella stessa unità del tasso. A tale proposito è fondamentale sapere che i e t si devono riferire sempre ambedue allo stesso periodo: ad esempio se t è in anni, i deve essere il tasso annuo.
Per un capitale unitario (dove C = 1), il fattore di capitalizzazione (o di montante) è quindi la funzione

Esempio
Calcolare il montante e gli interessi dell’investimento del capitale di euro 1.500 per 60 giorni al tasso di interesse annuo del 5%.

e pertanto gli interessi saranno (montante) 1.512,33 – (capitale) 1.500 = (interessi) 12,33€

Nel grafico è rappresentato l’andamento nel tempo dell’interesse la cui funzione ha equazione
I = 1.500 ∙ 0.05 ∙ t

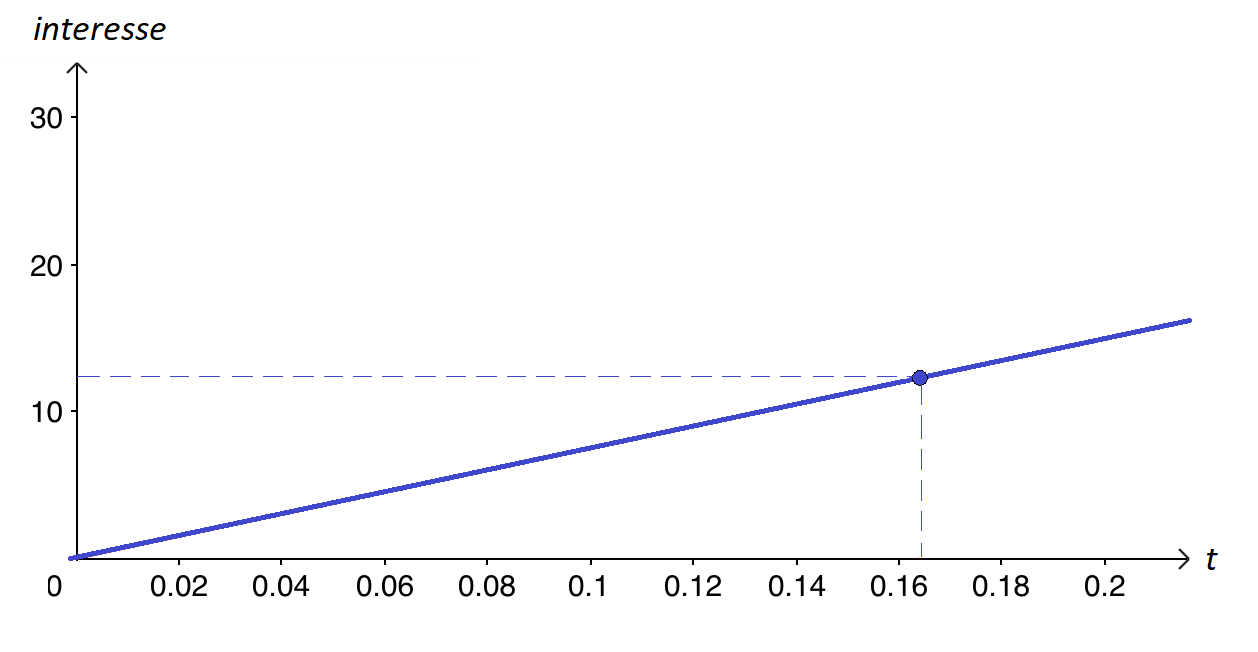
L’interesse ha andamento lineare rispetto al tempo t, ed il grafico risulta essere una retta passante per l’origine con coefficiente angolare Ci.
Queste stesse regole dell’interesse semplice possono essere utilizzate anche per attualizzare e scontare una certa somma a scadenza S, anziché capitalizzare e calcolare l’interesse su un capitale C, come abbiamo visto precedentemente.
Infatti si può avere anche il problema contrario, cioè sapere quanto bisogna “investire” per poter disporre di una somma ad una certa scadenza futura S e voler calcolare quanto questa somma valga oggi (V, valore attuale). Questa operazione si chiama attualizzazione, ovvero “andare indietro nel tempo” al contrario della capitalizzazione che “va avanti nel tempo”. La differenza tra la somma a scadenza ed il suo valore attuale è detta sconto D (quindi S – V = D).
Alle formule dello sconto ci si arriva facilmente se si pensa che dall’uguaglianza:
M = C (1 + i ∙t) deriva che

e quindi basta sostituire al capitale il valore attuale V ed al montante la somma a scadenza S per avere la formula del valore attuale

Questa relazione esprime il valore attuale della somma a scadenza, senza utilizzare lo sconto ed è anche detta formula dello sconto razionale.
Per conoscere l’entità dello sconto D si ha invece (sapendo che D = S – V):

Anche qui, nelle operazioni di attualizzazione, è bene memorizzare il fattore di attualizzazione, cioè la funzione che esprime il valore attuale V in caso di somma a scadenza pari a 1 (S = 1): 

Se si considera il tasso i per un anno su una somma a scadenza di 1 euro lo sconto razionale D, essendo S=1 e t=1, sarà:

Siccome lo sconto per S=1 e t=1 è il valore attuale di 1 € riscuotibile tra un anno, esso corrisponde al tasso di sconto d, quindi si ottiene:

da cui si ricava 

Queste relazioni tra tasso di sconto e tasso di interesse, valgono anche per gli altri regimi finanziari e la seconda consente di esprimere le formule di attualizzazione e di calcolo dello sconto razionale ottenute in funzione del tasso di sconto, sostituendo i con la sua espressione in d:

Mentre con d il tasso di attualizzazione v diventa:

Esempio

Trovare il valore attuale e lo sconto di una somma di euro 2.000 disponibile fra 30 giorni al tasso di interesse annuo del 5% ed al tasso di sconto annuo del 4,76%.

cioè (somma a scadenza) 2.000 – (valore attuale) 1.991,81 = 8,19 €

Se si ragiona con il tasso di sconto annuo:

I valori trovati sono gli stessi, perché in questo caso tra i e d c’è la corrispondenza vista sopra:

L’interesse commerciale

Il regime dello sconto commerciale è nato dall'usanza dei mercanti medievali di applicare direttamente, nelle operazioni di sconto, la formula con il tasso di sconto d (come se fosse il tasso di interesse i ), cioè: S ⋅d⋅ t senza passare per il tasso di interesse e lo sconto razionale (vigente nel regime di capitalizzazione semplice).
Era una grossa semplificazione nei calcoli, però, da un punto di vista matematico, non è la stessa cosa (perché i 2 tassi, di sconto e di interesse, non sono equivalenti) e di fatto quindi i mercanti dell’epoca hanno creato un altro regime, diverso da quello dell’interesse semplice, detto appunto “commerciale” perché usato nei calcoli dei commerci.
Pertanto si ha che lo sconto, in questo regime commerciale, è uguale a D = S⋅ d⋅ t
Di conseguenza la formula del valore attuale è (sempre ricordando che V = S – d) 

V = S⋅(1 –d⋅ t)

Il fattore di attualizzazione v per questo regime è v = 1 –d ⋅t
Questo regime commerciale è scarsamente utilizzato e le corrispondenti formule di capitalizzazione risultano ai più anche sconosciute.
Esclusivamente per completezza ne diamo comunque una quantificazione.
La capitalizzazione è:

Mentre la formula dell’interesse è:

Per concludere il fattore di capitalizzazione r è:

Le operazioni di attualizzazione in funzione di i anziché di d sono inutili. Tuttavia forniamo anche queste.
Il valore attuale è dato dalla seguente formula:

Lo sconto commerciale è uguale a:

Osservazione

Alcune delle funzioni trovate per determinati valori del tempo t possono annullarsi o tendere a +∞.

Ad esempio :

• nell’attualizzazione, più ci si avvicina al tempo limite t =1/d, più i valori tendono a zero, fino ad annullarsi proprio in questo punto (per poi assumere segno negativo)
• nella capitalizzazione, più ci si avvicina al tempo limite t = (1 + i)/i e più i valori assumono grandezze estreme, tendendo a infinito: come mostrato nel seguente grafico

L’andamento nel tempo dell’interesse è la funzione d'equazione

cioè una funzione omografica non definita per x = (1 + i)/i, valore che annulla il denominatore, e avente asintoto verticale la retta x = (1 + i)/i. Quindi y tende all'infinito per x che tende a (1 + i)/i.

Esempio 1

Determinare il valore attuale di una somma di euro 2.000 disponibile fra 30 giorni al tasso di sconto annuo del 5% in regime commerciale.

Esempio 2

Trovare il montante dell’investimento del capitale di euro 1.500 per 60 giorni al tasso di interesse annuo del 5% in regime commerciale.

L’interesse composto

Il regime dell’interesse composto è la percentuale sul capitale che si forma quando gli interessi maturati sono aggiunti al capitale e producono a loro volta degli interessi. Viene utilizzato per esempio dalle banche per costruire i piani d’ammortamento dei mutui.

Il suo elevato utilizzo è dovuto alla presenza di una caratteristica molto efficiente sia sul piano teorico, sia sul piano pratico delle esigenze concrete di chi capitalizza o attualizza: la scindibilità.
Consideriamo inizialmente la formula della capitalizzazione composta, perché se per altri regimi si poteva iniziare dalla formula degli interessi I, ora è preferibile comprendere e memorizzare prima di tutto la formula di M. Nel regime finanziario a interesse composto si considera che, alla fine di ogni periodo, l'interesse maturato nel periodo debba essere sommato al capitale, per costituire così un nuovo capitale su cui calcolare gli interessi nel periodo successivo. 
Considerando che il montante è proprio la somma di capitale e interessi maturati, possiamo dire che nel regime a interesse composto il montante al tempo t viene assunto come nuovo capitale per il periodo successivo.

Procedendo nel modo indicato per più periodi, è possibile ricavare la formula che descrive questo regime. Se si assume ogni periodo di durata unitaria si ha

alla fine del primo periodo: M (1) = C (1)∙( 1 + i )
alla fine del secondo periodo: M (2) = M (1)∙( 1 + i ) = C∙( 1 + i )²
e così via. In generale, alla fine periodo t si avrà: M = C∙(1 + i)^t
Da questa relazione si ricava quella degli interessi I, che è molto semplicemente la sua differenza con C, cioè:
I = C ∙[(1 + i)^t – 1]
Il fattore di capitalizzazione r è quindi:
r = (1 + i)^t
Ricordando che se M = C r , allora C = m⁄r , e pertanto, sostituendo opportunamente M con S e C con V, si ha:

e anche:

Il fattore di attualizzazione v, anche in questo regime, è il reciproco di r, ovvero:

Anche se non sono molto usate nell’ambito dell’interesse composto, si riportano anche le formule di attualizzazione con il tasso di sconto d al posto di quello di interesse i

• per l’attualizzazione: V = S ∙(1-d)^t
• per lo sconto: D = S ∙[ 1-(1-d)^t]

ESEMPIO 1
Calcolare il montante di un capitale di 2.500 euro capitalizzato in regime composto per 5 mesi al tasso di interesse annuo del 15%.

ESEMPIO 2
Calcolare il valore attuale di un capitale di euro 2.649,91 in regime composto per 5 mesi al tasso di sconto annuo del 13,04348%.

 
Nel grafico è rappresentato l’andamento esponenziale nel tempo dell’interesse la cui funzione ha equazione y=C∙[(1+i)^x–1]

Per ricavare il tempo del periodo d’investimento, partendo da montante, interesse, valore attuale, o sconto, bisogna utilizzare i logaritmi.

Ad esempio per calcolare il tempo di investimento sapendo che il montante di un capitale di 2.500 euro è 2.650, capitalizzato in regime composto al tasso di interesse annuo del 15%, dalla formula del montante M=C∙(1 + i)^t si ricava la formula inversa per il calcolo del tempo:

 

in mesi:

Tassi equivalenti

Quando la capitalizzazione o l'ammortamento non avvengono annualmente, ma con cadenze più frequenti (ad esempio mensile, trimestrale,..) è necessario determinare il tasso riferito al periodo in modo che sia equivalente al tasso annuale. 

Per determinare la relazione tra i due tassi unitari ad interesse composto annuale i e im equivalente è sufficiente uguagliare i montanti che sono prodotti da periodi di tempo t e m differenti: 

M = C∙(1 + i)^t e M_m= C∙(1 + i_m)^m   →  C∙(1 + i)^t = C∙(1 + i_m)^m   →   (1 + i)^t =(1 + i_m)^m

dove t = 1 (1 anno).
Si possono ricavare da qui l’equivalenza finanziaria dei tassi di interesse 1 + i = (1 + i_m)^m e le formule per il calcolo dell’interesse annuale

i = (1 + i_m)^m-1

e dell’interesse equivalente

(dove i_m è il tasso di interesse riferito al periodo infrannuale m).

Pertanto significa che:
m = 12 tasso mensile;
m = 3 tasso quadrimestrale;
m = 4 tasso trimestrale;
m = 2 tasso semestrale;
m = 1 tasso annuale
Le suddette uguaglianze non dicono altro che, vista la scindibilità del regime, per avere il montante di un capitale pari ad 1 dopo un anno, bisogna applicare la capitalizzazione al tasso periodico m per il numero dei periodi m compresi nell’anno. Ad esempio per m=12 (tasso mensile) si ha: 1 + i = (1 + i₁₂)¹² che è facilmente comprensibile in quanto vuol dire che capitalizzando per 12 mesi al tasso mensile, si ottiene il montante della capitalizzazione annuale al tasso annuale.

ESEMPIO 1
La Banca propone un tasso di interesse annuale i = 27%. Calcola il tasso mensile  i₁₂ equivalente.

ESEMPIO 2

La Banca propone un tasso di interesse trimestrale   i₁₂= 1%. Calcola il tasso annuo i equivalente.

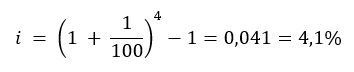
Il tasso nominale

Il tasso di interesse nominale è il prodotto del tasso periodico i_m con m, cioè j_m = i_m ∙ m.

Il tasso d'interesse nominale j_m è il tasso applicato in un atto o in un contratto di prestito, di finanziamento o di mutuo ed indica il costo teorico per chi prende a prestito del denaro ed il rendimento, teorico anch'esso, per chi lo presta.
Esso si affianca al tasso i visto finora, che prende, di conseguenza, il nome di effettivo.
Quest’ulteriore versione di tasso, è nato dalla pratica di molte banche di dichiarare al cliente prenditore di prestiti, anziché il tasso effettivo più alto, quello nominale, che fa sembrare (appunto nominalmente) il costo del finanziamento più basso di quanto lo sia in realtà (perché comunque il tasso di interesse su cui esso è calcolato è sempre quello effettivo). Adesso le banche devono quindi, per legge, dichiarare, accanto a quello nominale, il tasso di interesse effettivo del prestito proposto.
La formula inversa, per il calcolo di i_m dato j_m , è

e la relazione tra j_m e i annuo:

da cui

oppure

(importante perché permette di calcolare il tasso di interesse effettivo quando si è a conoscenza del tasso nominale).

ESEMPIO
La banca dà un prestito al 10% di interesse nominale annuo, con rata di rimborso mensile. Quanto costerà effettivamente il credito concesso dalla banca?

Conclusioni

Il calcolo degli interessi non è quindi univoco, ma dipende dal “regime finanziario” che si va ad applicare. La seguente tabella sintetizza le formule per il calcolo degli interessi

Calcolo interessi e montante

Di seguito il file realizzato con GeoGebra per il calcolo nei tre regimi dell'interesse e del montante, dati periodo, tasso d'interesse annuale e capitale (inserire i valori nelle celle colorate) e il confronto grafico dell’andamento nel tempo dei tre metodi di applicazione:

Variare i dati (periodo, tasso d'interesse annuale e capitale) muovendo gli slider:

Dal grafico sopra riportato si possono trarre importanti conclusioni per la capitalizzazione:

• nei periodi inferiori all’anno, per il creditore che fa fruttare una somma di denaro, è più conveniente il regime dell’interesse semplice. Infatti si ha che per t<1 Interesse Semplice > Interesse Composto >Interesse Commerciale
• nei periodi superiori all’anno, per il creditore è invece più conveniente il regime dell’interesse commerciale. Infatti si ha che per t>1 Interesse Commerciale> Interesse Composto >Interesse Semplice

Ricordiamo però che nello sconto commerciale deve sempre valere la condizione t <1/d perché altrimenti i valori tendono all’infinito e nell’attualizzazione i valori diventano negativi.