Scale musicali

Come spiegato nel capitolo sulla risposta logaritmica dell'udito, il suono è la sensazione data dalla vibrazione di un corpo in oscillazione. Tale vibrazione, che si propaga nell'aria o in un altro mezzo elastico, raggiunge l'apparato uditivo e crea una sensazione "uditiva" correlata alla natura della vibrazione. Le oscillazioni sono spostamenti delle particelle intorno alla posizione di riposo e lungo la direzione di propagazione dell'onda; gli spostamenti sono provocati da movimenti vibratori, provenienti da un determinato oggetto, chiamato sorgente del suono, il quale trasmette il proprio movimento alle particelle adiacenti grazie alle proprietà meccaniche del mezzo; le particelle iniziando ad oscillare, trasmettono il movimento alle altre particelle vicine e queste a loro volta ad altre ancora, provocando una variazione locale della pressione; in questo modo, un semplice movimento vibratorio si propaga meccanicamente originando un'onda sonora. Per le onde sonore, l'ampiezza dell'onda è la differenza tra la pressione del mezzo non perturbato e la pressione massima causata dall'onda.

Come tutte le onde, anche quelle sonore sono caratterizzate da una frequenza, un'intensità (che è in relazione con il cosiddetto "volume" del suono) e dalla forma d'onda stessa, da cui dipende il timbro che caratterizza le diverse tipologie di suono, permettendo di distinguere suoni emessi da sorgenti diverse, anche se essi hanno la stessa frequenza e la stessa intensità. Ciascun strumento musicale ha un timbro diverso.

L'altezza (o Acutezza) è la caratteristica legata alla rapidità delle vibrazioni delle onde che producono il suono e ci consente di distinguere i suoni acuti da quelli gravi. Essa cambia a seconda della frequenza a cui l’onda vibra: al crescere della frequenza corrisponde l’aumento dell’altezza. La frequenza è una grandezza che riguarda fenomeni periodici o processi ripetitivi. 

L'intensità acustica o sonora è una grandezza fisica definita come il rapporto tra la potenza di un'onda sonora e l'area della superficie che da essa viene attraversata; oppure come l'energia che nell'unità di tempo attraversa l'unità di superficie posta in un punto perpendicolarmente alla direzione di propagazione del suono. È la grandezza che permette di distinguere i suoni deboli da quelli forti, un suono è tanto più forte quanto maggiore è l’ampiezza delle oscillazioni della sorgente che lo genera. 

I suoni esistenti in natura sono complessi, ma scomponibili in una serie di suoni puri detti armonici. Gli armonici sono generati spontaneamente dalle vibrazioni dei corpi elastici, (per esempio, la corda degli strumenti musicali) e hanno frequenze che variano tra 37Hz e 4685Hz. Le note della scala musicale (do, re, mi, fa, sol, la, si) si distinguono l’una dall’altra per la frequenza, ovvero il numero delle vibrazioni al secondo che un corpo elastico può emettere. Si parla di scala musicale perché, aumentando il numero delle vibrazioni, i suoni diventano più acuti salendo in altezza, come rappresentato dalla seguente figura.

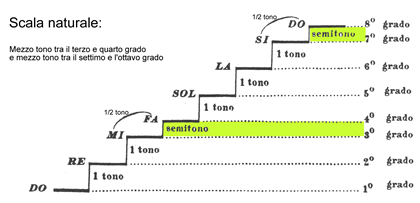
Il suono emesso da un diapason può essere considerato un suono puro. 

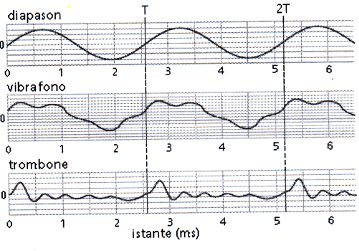
Varia frequenza e ampiezza e clicca su Ascolta il suono.

Nella teoria musicale, una scala è una successione di 8 suoni, di cui l'ultimo è una ripetizione del primo. Si chiama scala ascendente una scala in cui l'altezza delle note cresce, e scala discendete una in cui l'ordine è decrescente. Le scale conosciute sono numerose: scale diverse hanno un diverso numero di suoni e diverse specie di intervalli. Popolazioni diverse adoperano scale diverse e una stessa popolazione può aver adottato differenti scale nel corso della storia, per motivi culturali e per l'utilizzo di differenti sistemi di accordatura. 

Storia delle scale musicali 

In ogni area culturale e in ogni epoca si sono formati diversi sistemi musicali, e ogni sistema ha una scala che lo caratterizza.

Il più antico procedimento per dividere l'ottava in un dato numero di parti risale ai primi tempi dell'antica civiltà cinese. In seguito fu utilizzato dai teorici giapponesi e, con autonoma ideazione, dai pitagorici. Pitagora basò la sua dottrina sui numeri interi e, studiando la musica, scoprì come le altezze dei suoni fossero legate fra loro da rapporti di numeri interi, ovvero da numeri razionali.

Secondo un aneddoto la scoperta avvenne percuotendo un'anfora ripiena d'acqua che poi, riempita ulteriormente, emetteva la stessa nota ma più acuta. Esistono diverse varianti dell'aneddoto: Giamblico di Calcide, ad esempio, raccontò che l'intuizione di Pitagora sarebbe merito di un fabbro che martellava il ferro con mazze di grandezze diverse. Tra i tintinnii che venivano prodotti dai colpi alcuni risultavano più gradevoli di altri. Fu così che Pitagora scoprì che i martelli i cui pesi stavano in precisi rapporti producevano dei suoni consonanti, cioè eseguiti simultaneamente erano tali che l'effetto complessivo risultasse morbido e gradevole.

Le consonanze fra i suoni furono studiate dai pitagorici analizzando i suoni prodotti dal monocordo, uno strumento costituito da una corda tesa tra due estremi fissi, al di sotto della quale scorre liberamente un ponticello mobile che divide la corda in due segmenti di lunghezza variabile. Ascoltando il suono prodotto da questi due segmenti di corda, secondo i pitagorici, si otteneva un suono consonante solo quando, dal rapporto tra le misure delle due parti, risultava una frazione costituita da due numeri interi piccoli. Ponendo il ponticello mobile a metà della lunghezza della corda (o premendola a metà) e pizzicando una delle sue metà, si ottiene un nota ad un'ottava superiore.

Quindi se si chiama Do la nota emessa dalla corda libera, dimezzandola si ottiene il Do all'ottava superiore. 

Riducendo la corda ai suoi 2/3 si ottiene, invece, l'intervallo di quinta giusta. Quindi in tal modo si ottiene un Sol. Analogamente, prendendo due corde uguali ma lunghe una il triplo dell'altra, si producono suoni distanti una quinta ma in due ottave differenti.                                                                                     

I pitagorici partirono dai rapporti numerici corrispondenti agli intervalli consonanti di ottava, quinta e quarta e, scelta una nota di riferimento, iniziarono a generare le altre note della scala attraverso un procedimento per quinte ascendenti e discendenti. In quest'ultimo caso le note vengono generate dividendo la frequenza della nota di partenza per 3/2, in quello per quinte ascendenti, invece, moltiplicando la frequenza per 3/2. Dalla seconda moltiplicazione però, si ottengono frequenze di suoni che si trovano all'ottava superiore rispetto quella che contiene la nota di riferimento. Per riportare tali frequenze nell'ambito dell'ottava di partenza si divide la frequenza così ottenuta per 2ⁿ, dove n è il numero di ottave che si sono ''percorse''. Analogamente, nel procedimento per quinte discendenti si trovano frequenze nelle ottave inferiori rispetto a quella che contiene la nota di partenza, e per riportarle nell'ottava di partenza si moltiplica la frequenza ottenuta per 2ⁿ.

Matematicamente possiamo riassumere la regola generativa con la seguente espressione:

dove r_k rappresenta la nota ottenuta attraverso il procedimento per quinte (ascendenti o discendenti) descritto, n il numero di ottave che distano da quella di partenza e Z_k la nota ottenuta riportata nell'ottava di partenza. Se k è positivo si sta applicando il procedimento per quinte ascendenti, se è negativo quello per quinte discendenti.

Ad esempio, cominciando dal Do₂ si costruisce la progressione delle quinte (Sol₂, Re₃, La₃, Mi₄, Si₄) e si dividono per un'ottava le note che si trovano ad ottave superiori a quella di partenza (Re₃ diventa Re₂, La₃ diventa La₂ e così via). 

moltiplicazione per 3/2 della precedente	controllo ottava	riporto alla prima ottava ottava	in frazione	Rapporto	Formula generativa	Nota
1	<2	1		1:1		Do
1,5	<2	1,5	3/2	3:2	3/2	+5=Sol
2,25	>2 dividere per 2	1,125	9/8	9:8	(3/2)^2:2	+5=Re
3,375	>2 dividere per 2	1,6875	27/16	27:16	(3/2)^3:2	+5=La
5,0625	>4 dividere per 4	1,265625	81/64	81:64	(3/2)^4:2^2	+5=Mi
7,59375	>4 dividere per 4	1,8984375	243/128	243:128	(3/2)^5:2^2	+5=Si

Per ottenere il Fa si deve invece scendere di una quinta (Fa₁) e si sale di un'ottava in modo da ricondursi all'ottava di partenza (Fa₁ diventa Fa₂).

Scala temperata

La differenza in altezza tra due suoni musicali, costituita dalla differenza di numero delle loro vibrazioni, si chiama intervallo. L'intervallo si determina contando le linee e gli spazi che separano le due note sul rigo musicale. Due intervalli sono uguali se è uguale il rapporto (e non la differenza) delle frequenze dei suoni dell'intervallo.

Alla fine del XVII sec. Andreas Werckmeister adottò, per costruire una scala, un procedimento matematico molto rigido rispetto ai criteri di ricerca precedenti: partendo dall'intervallo di un'ottava divise la scala in dodici parti uguali. Trovò in tal modo un coefficiente, una costante: la radice dodicesima di due, il cui valore è approssimato a 1,059.

Il rapporto fra la frequenza di una nota e la successiva è costante ed è detto semitono temperato. Indicando con x il valore del semitono temperato, possiamo scrivere:

 

dove: # rappresenta il diesis e b il bemolle.

La scala delle frequenze è una progressione geometrica di ragione x.

Inoltre è possibile notare che la frequenza di una qualsiasi nota di un’ottava raddoppia nell’ottava successiva:

da cui si ottiene  f(do2)=2f(do). Perciò, visto che la ragione q di una progressione geometrica a_n=a₀qⁿ è data da:

si ottiene

che si può approssimare a 1,06.

Dunque, moltiplicare la frequenza di una nota per  2^1/12 corrisponde a salire di un semitono nella scala temperata, come rappresentato in figura.

 

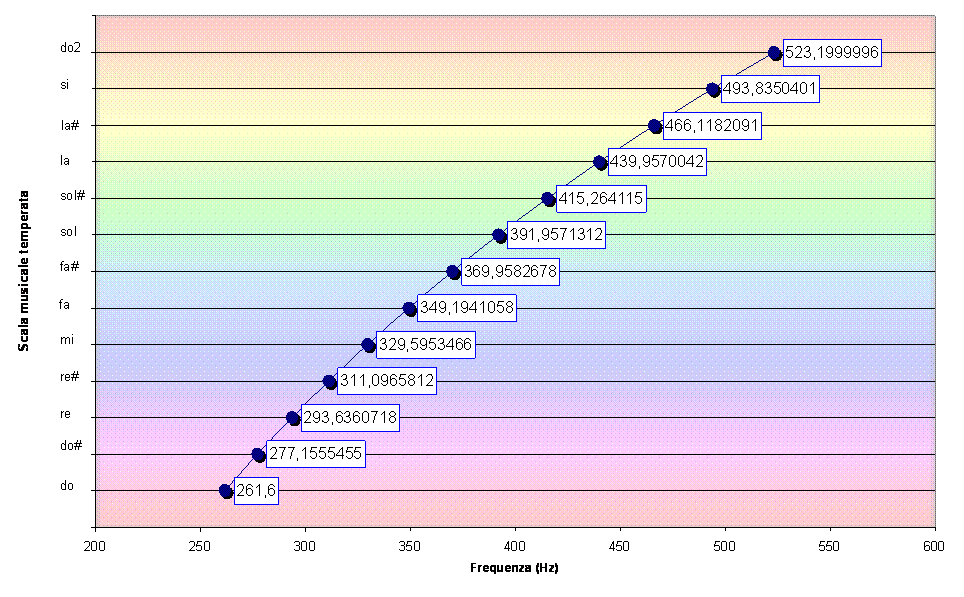
Se si vuole conoscere quanti semitoni corrispondono ad un dato rapporto di frequenza rf è necessario risolvere l'equazione esponenziale

in cui n rappresenta il numero dei semitoni e la cui soluzione è

Inoltre, per la proprietà dei logaritmi – “il logaritmo di un quoziente è uguale alla differenza dei logaritmi del dividendo e del divisore”, la scala logaritmica trasforma i rapporti di frequenza in differenze, così un’ottava si traduce in un intervallo costante fra i logaritmi delle frequenze:

 … e così via.

Se i logaritmi sono in base 2, il numero risultante dalla differenza dei logaritmi è l’intervallo tra le note espresso in ottave, perché 2 è il rf (rapporto di frequenza) dell’ottava. Se i logaritmi sono in base 2^1/12  allora il numero risultante è l’intervallo espresso in semitoni, perché 2^1/12 è il rf (rapporto di frequenza) del semitono temperato.

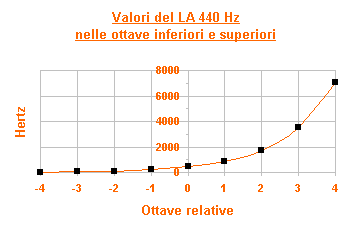Dal grafico, nell'esempio riferito alla nota LA (440 Hz) ma valido nella forma per qualsiasi altra nota, si evince che l'andamento delle frequenze musicali è di tipo logaritmico.

Nel 1880 il musicologo inglese Alexander Ellis introdusse una suddivisione più piccola per valutare le piccole differenze di intonazione: il cent. Il cent corrisponde ad un centesimo di semitono, ovvero la milleduecentesima parte di un’ottava. Anche il centesimo di un semitono è in scala logaritmica e, quindi, è una misura moltiplicativa e non additiva, cioè se 1cent =2 allora 3cent=8 .

In questo caso il rapporto di frequenza rf che corrisponde ad 1 cent è:

 

Il "cent" oggi è universalmente accettata come unità di misura degli intervalli musicali, è un'unità di misura logaritmica; infatti deriva dalla divisione dell'ottava in 1200 parti proporzionali. Il rapporto fra due frequenze pari a 1 cent è 1.00057779 e corrisponde a 2^(1/1200), ovvero alla radice milleduecentesima di 2. Le formule di conversione per passare da cents a rapporti e viceversa, indicando con C i cents e con rf i rapporti, sono:

C = 1200 log₂rf = 3986.313714 log₁₀ rf    

rf = 2 ^(C/1200)

Nella seguente tabella si riportano le frequenze delle note, ottenute partendo da 440HZ del La e le ampiezze degli intervalli in cent.

Nota	rapporto	Frequenza (Hz)	rapporto di frequenza rispetto al Do (in cent)
Do3	1	261,6	0
Do# o REb	21/12	277,2	100
Re	22/12	293,7	200
Re# o Mib	23/12	311,1	300
Mi	24/12	329,6	400
Fa	25/12	349,2	500
Fa# o Solb	26/12	370,0	600
Sol	27/12	392,0	700
Sol# o Lab	28/12	415,3	800
La	29/12	440,0	900
La# o Sib	210/12	466,2	1000
Si	211/12	493,9	1100
Do4	212/12=2	523,3	1200

I calcoli sono stati svolti con excel:

		Nota	rapporto	Frequenza (Hz)	rapporto di frequenza rispetto al Do (in cent)
0	-9	Do3	1	=$L$12*2^(I3/12)	0
=H3+1	=I3+1	Do# o REb	21/12	=$L$12*2^(I4/12)	=1200*LOG(2^(H4/12);2)
=H4+1	=I4+1	Re	22/12	=$L$12*2^(I5/12)	=1200*LOG(2^(H5/12);2)
=H5+1	=I5+1	Re# o Mib	23/12	=$L$12*2^(I6/12)	=1200*LOG(2^(H6/12);2)
=H6+1	=I6+1	Mi	24/12	=$L$12*2^(I7/12)	=1200*LOG(2^(H7/12);2)
=H7+1	=I7+1	Fa	25/12	=$L$12*2^(I8/12)	=1200*LOG(2^(H8/12);2)
=H8+1	=I8+1	Fa# o Solb	26/12	=$L$12*2^(I9/12)	=1200*LOG(2^(H9/12);2)
=H9+1	=I9+1	Sol	27/12	=$L$12*2^(I10/12)	=1200*LOG(2^(H10/12);2)
=H10+1	=I10+1	Sol# o Lab	28/12	=$L$12*2^(I11/12)	=1200*LOG(2^(H11/12);2)
=H11+1	=I11+1	La	29/12	440	=1200*LOG(2^(H12/12);2)
=H12+1	=I12+1	La# o Sib	210/12	=$L$12*2^(I13/12)	=1200*LOG(2^(H13/12);2)
=H13+1	=I13+1	Si	211/12	=$L$12*2^(I14/12)	=1200*LOG(2^(H14/12);2)
=H14+1	=I14+1	Do4	212/12=2	=$L$12*2^(I15/12)	=1200*LOG(2^(H15/12);2)

Rispetto ai rapporti di frequenze, la conversione in cents consente di effettuare con semplicità le operazioni di addizione, sottrazione e confronto fra gli intervalli, tipica delle unità di misura logaritmiche. Adottando la scala logaritmica l'ampiezza dell'intervallo complessivo è uguale alla somma delle ampiezze dei sottointervalli da cui è costituito. Infatti se il primo intervallo ha misura

e il secondo intervallo ha misura

e l'intervallo ottenuto "raccordando" i due intervalli ha misura

poichè si ha

allora

Considerando poi che la minima variazione di altezza percepibile dall’orecchio umano è circa 2 cents in particolari condizioni di ascolto e circa 10 cents durante le esecuzioni musicali "dal vivo", il risultato della conversione da rapporti a cents può essere arrotondato all'intero più vicino, semplificando ulteriormente le operazioni matematiche.

Infine per determinare la frequenza in Hertz è possibile utilizzare la formula relazione:      

 

dove:

• f_x è il valore di frequenza desiderato
• f₀ è la frequenza, in hertz, della nota di riferimento (es. LA = 440 Hz)
• C_x è il valore, in cents, della nota di cui si desidera conoscere la frequenza
• C₀ è il valore, in cents, della nota di riferimento (es. LA = 900 cents)

Le note di una scala sono definite anche gradi e nel nostro sistema a seconda della posizione che occupano hanno un nome che indica la loro funzione nella scala:

• I grado - tonica: è la nota iniziale della scala;
• II grado - sopratonica;
• III grado - mediante (o modale): determina il carattere della scala, cioè se è maggiore o minore;
• IV grado - sottodominante;
• V grado - dominante: è il grado più importante dopo la tonica, viene chiamata in tal modo poiché è la nota dominante della scala;
• VI grado - sopradominante
• VII grado - sensibile o sottotonica: la sensibile tende a risolvere sulla tonica, e si trova in tutte le scale eccetto che nella scala minore naturale e nella scala melodica discendente (vedi par. le scale musicali) in cui prende il suo posto la sottotonica.

La distanza tra due gradi consecutivi può essere di tono o di semitono, ciò dipende dalla posizione che occupano nella scala considerata. Nel nostro sistema, il sistema temperato equabile, il semitono è la metà di un tono, e tale distanza può essere ascoltata suonando due tasti consecutivi di un pianoforte.

Esistono due tipi di semitono:

• semitono cromatico: formato da due note con lo stesso nome ma diversa altezza (es: Do - Do#, Mib - Mi)^;
• semitono diatonico: formato con due note consecutive con diverso nome e diversa altezza (es: Fa# - Sol, La - Sib)

La musica occidentale si basa sul sistema temperato equabile. La sua scala si distingue anzitutto in cromatica e diatonica.

La scala cromatica è la scala che comprende tutti i suoni possibili del sistema, quindi nel temperamento equabile è definita dalla successione di 12 semitoni contigui.

La scala diatonica è una scala di 7 note e ad essa appartengono due grandi tipi di scale:

• la scala maggiore, costituita da 5 toni e 2 semitoni

• la scala minore che si presenta in tre diverse forme:
  • La scala minore naturale, costituita anch'essa da 5 toni e 2 semitoni , questi ultimi disposti tra il II e III grado e tra il V e il VI;
  • la scala minore armonica, costituita da 3 toni, 3 semitoni
  • la scala minore melodica, costituita da 5 toni e 2 semitoni sia nel moto ascendente che in quello discendente, ma mentre nel moto ascendente i semitoni si trovano l'uno tra il II e il III grado (come nel moto discendente) e l'altro tra il VII e l'VIII, in quello discendente quest'ultimo semitono si sposta fra VI e V grado.

Creazione di una tastiera attraverso il programma Geogebra

• Dalla barra strumentale, selezionare la casella “Punto” e posizionarlo in una posizione definita del piano.

• Ripetere lo stesso passaggio per i 4 punti esterni della pianola ed unirli con il comando “segmento” in modo da formare un rettangolo.

• Successivamente, suddividere la figura creata in 7 colonne, le quali delineeranno i 7 tasti chiari (toni) del pianoforte. 
  

• Attraverso il medesimo procedimento utilizzato per creare i toni, delineare dei rettangoli tra le colonne dei toni che andranno a formare i semitoni (il colore nero può esser assegnato tenendo premuto sul semitono e selezionando “Impostazioni”). Il risultato dovrebbe essere simile a quello in figura.

• Attraverso la barra strumenti, selezionare il comando “Pulsante” e ripetere lo stesso procedimento per ogni nota, contrassegnandola con il relativo nome (Do,Re, Mi..); in seguito, posizionare il pulsante sul comando corrispondente a ogni nota. 

• Schiacciando su ogni pulsante, selezionare l’opzione “Proprietà-Scripting-AlClik” e inserire la funzione Suono(funzione, Valore min, Valore max) dove funzione è sin(2pfx), con f è la frequenza della nota considerata, valore min e max definiscono l'intervallo di tempo. Per esempio per riprodurre un tono di un'onda sinusoidale pura a 440 Hz (nota musicale La), per un secondo

 Ed ora possiamo finalmente suonare: