La spirale logaritmica

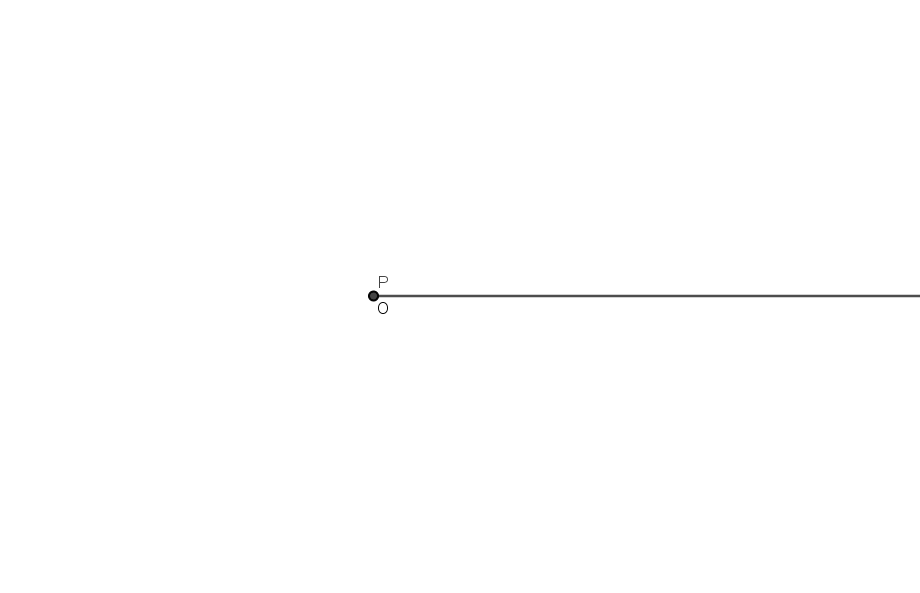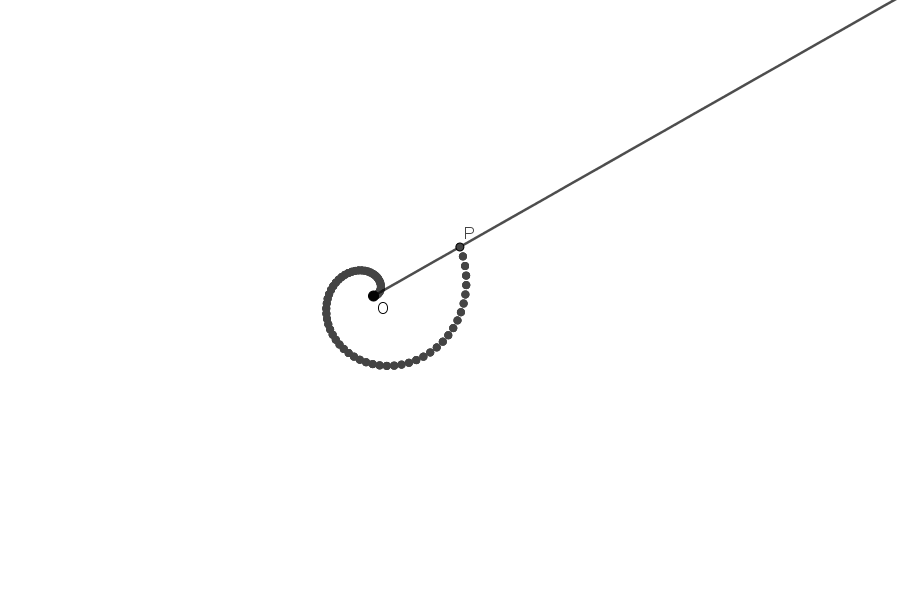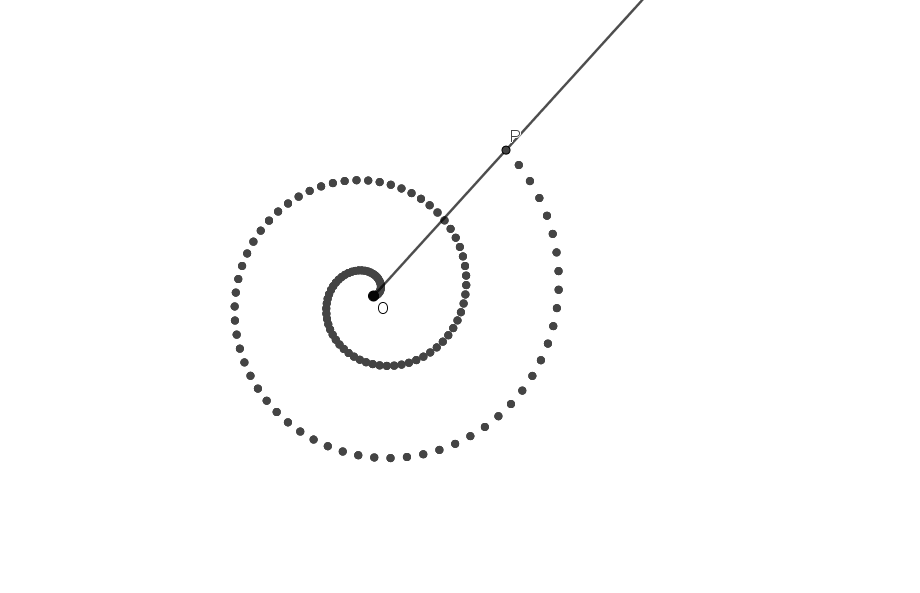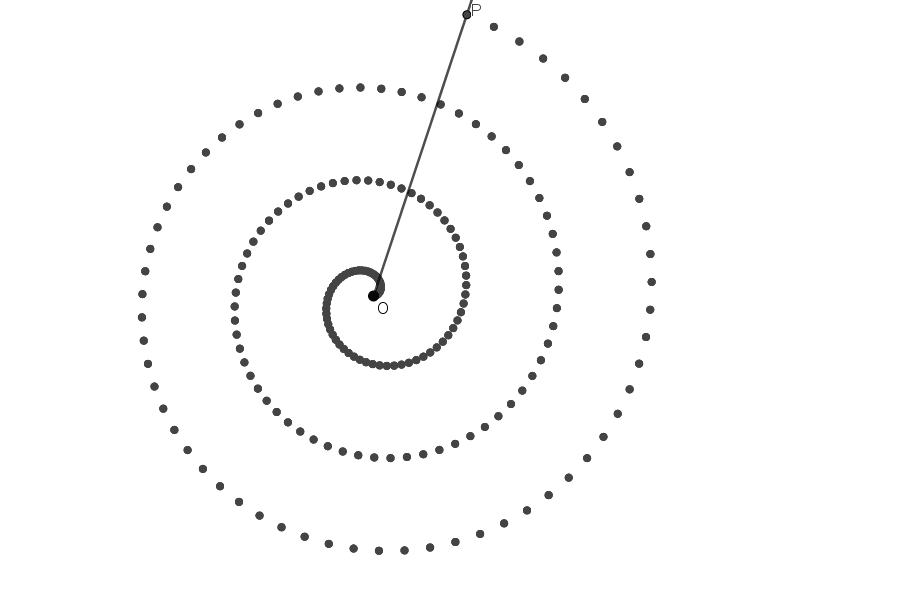
La curva spirale è la traiettoria disegnata da un punto P che si muove su una semiretta allontanandosi o avvicinandosi alla sua origine O, mentre la semiretta ruota attorno alla sua origine O.

Ricomincia l'animazione

Vi sono spirali bidimensionali e tridimensionali (ad esempio i vortici o le eliche). Una spirale bidimensionale può essere descritta usando le coordinate polari e imponendo che il modulo r sia una funzione continua e monotona dell’anomalia θ.

Le coordinate polari

Le coordinate polari costituiscono un sistema di coordinate nel piano della forma (r, θ) in cui ogni punto P del piano viene individuato univocamente dalla distanza r da un punto fisso O, detto polo, e dall’ampiezza in radianti θ dell’angolo avente vertice nel polo, primo lato una semiretta fissa avente origine nel polo, detta asse polare e secondo lato la semiretta avente origine in O e passante per P.

Coordinate polari e coordinate cartesiane

Se si fissano in un piano un sistema di riferimento cartesiano e uno polare in modo che l’origine del cartesiano coincida con il polo del polare e il semiasse positivo delle ascisse sia l’asse polare, dato un punto P e dette (x;y) le sue coordinate cartesiane e (r, θ) le sue coordinate polari si ha per il teorema di Pitagora e per i teoremi sui triangoli rettangoli:

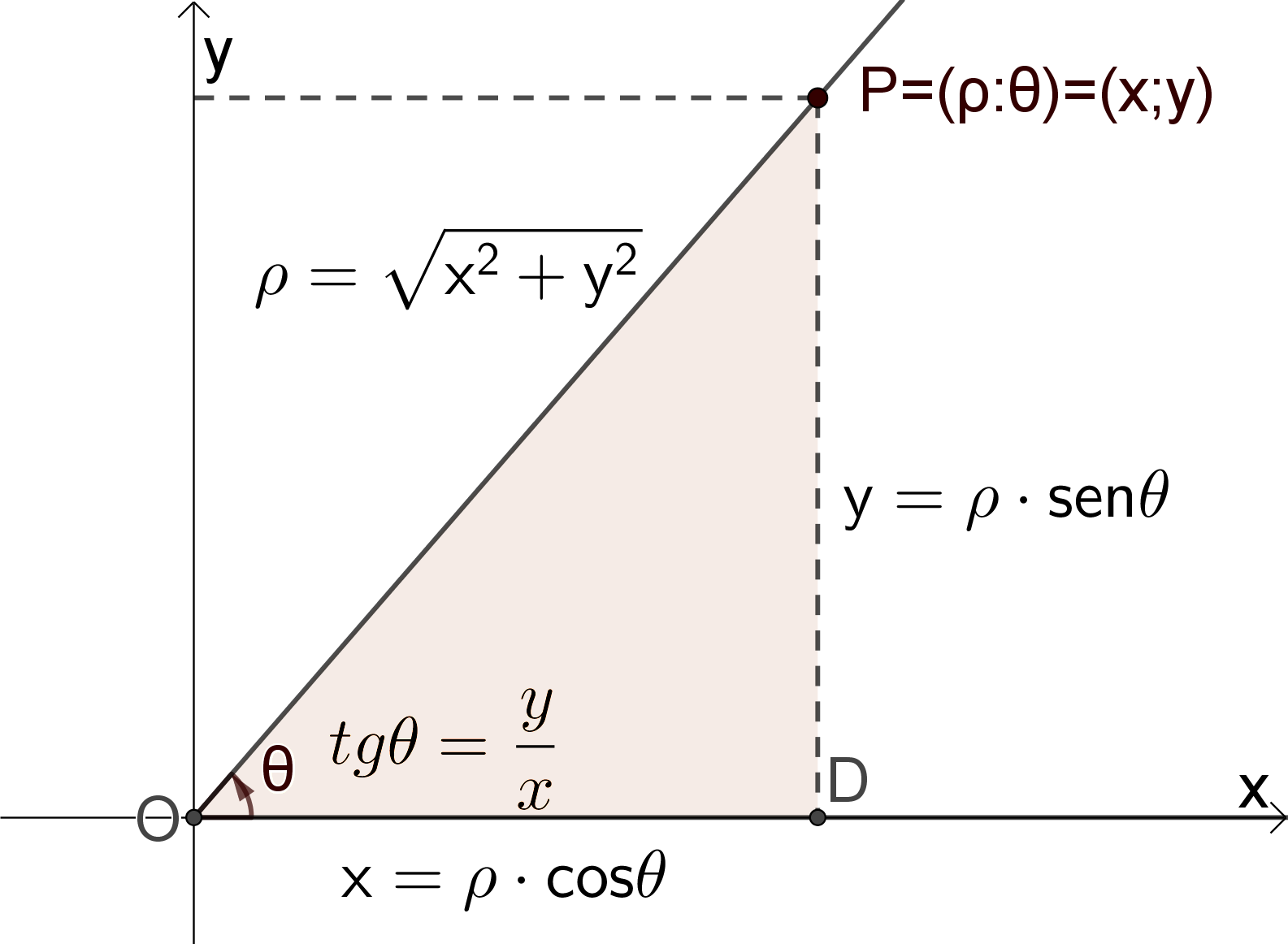
Per determinare le coordinate cartesiane, note quelle polari:

Per determinare le coordinate polari, note quelle cartesiane:

facendo attenzione per la determinazione di θ al quadrante in cui si trova P.

Spirali

La spirale bidimensionale più comune è quella uniforme, detta di Archimede (o anche evolvente), definita come la traiettoria descritta da un punto che si muove con velocità uniforme su una semiretta che ruota uniformemente intorno al polo. Definendo la funzione r=f(θ) si ottengono diversi tipi di spirali bidimensionali tra le quali la spirale archimedea, la spirale di Fermat o parabolica, la spirale iperbolica, il lituo e la spirale logaritmica.

La spirale logaritmica

Una spirale logaritmica, o spirale equiangolare o spirale di crescita è un tipo particolare di spirale che si ritrova spesso in natura. La spirale logaritmica è stata descritta la prima volta da Cartesio (filosofo e matematico francese, La Haye en Touraine (oggi Descartes), 1596 – Stoccolma, 1650), e successivamente da Jakob Bernoulli (matematico e scienziato svizzero,  Basilea, 1654 – Basilea, 1705), che la definì Spira mirabilis, "la spirale meravigliosa", e ne volle una incisa sulla sua lapide. Tuttavia, venne incisa una spirale archimedea al suo posto.

La spirale logaritmica è la traiettoria di un punto che si muove di moto uniformemente accelerato su una semiretta, la quale ruota uniformemente intorno alla sua origine. 

In coordinate polari (r, θ) la curva ha equazione

con a e b numeri reali. Dall'equazione si ricava 

da cui il nome di spirale logaritmica.

In forma parametrica si ha:

Al variare del coefficiente a ruota la spirale cambiando l'ingrandimento mentre b controlla quanto è stretta e in quale direzione si avvolge. 

 

Mentre le lunghezze dei segmenti tra spire successive nella spirale archimedea sono costanti, nella spirale logaritmica aumentano secondo una progressione geometrica. Infatti due segmenti tra due spire successive sul semiasse positivo delle x (y=0→a^.b^q.senq=0→b^q=0 è impossibile, senq=0→q=kp e x>0→q=2kp) hanno ascisse

Utilizzando le equazioni parametriche della curva si ottengono le coordinate cartesiane dei punti di intersezione con l'asse delle ascisse: 

per cui 

Il rapporto è quindi costante rispetto a k, cioè è indipendente dalla scelta del primo punto: qualunque siano tre punti consecutivi di intersezione della spirale con l'asse delle ascisse il rapporto è sempre lo stesso. Le lunghezze dei segmenti tra spire successive sono quindi in progressione geometrica con la ragione che dipende soltanto dal parametro b dell'equazione della curva .

La successione di Fibonacci e la spirale aurea

La successione di Fibonacci, introdotta per la prima volta nel 1223 da Leonardo da Pisa (più noto come Fibonacci poiché filius Bonacci, il figlio di Bonaccio) come soluzione ad un problema proposto dall’Imperatore Federico II di Svevia ad un torneo di matematici. Il problema aveva per argomento la crescita di una popolazione di conigli in n mesi, ipotizzando che ogni coppia di conigli impieghi un mese per diventare adulta e un secondo mese per procreare un’altra coppia.

Ecco cosa accade alla popolazione della colonia dei conigli:

1. Nel primo mese, si ha la coppia di partenza.
2. Nel secondo mese, si ha la coppia di partenza, che nel frattempo è diventata pronta a generare un’altra coppia di conigli.
3. Nel terzo mese, la coppia di partenza ha generato una coppia di conigli, che non è ancora fertile. Quindi le coppie sono diventate 2 di cui una sola è fertile.
4. Nel quarto mese, la coppia di partenza ha generato un’altra coppia di conigli. La coppia ottenuta al passo 3 è diventata fertile, ma non ha ancora generato un’altra coppia. Quindi le coppie ora sono 3, di cui 2 fertili.
5. Nel quinto mese, le due coppie fertili hanno generato un’altra coppia ciascuna. Quindi le coppie di conigli sono diventate 5; le due coppie appena nate non sono fertili, mentre le altre 3 lo sono.

Fibonacci diede come risposta 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144 , 233 , 377 , ..... dove ogni numero della successione si ottiene addizionando i due che lo precedono (con l'esclusione dei primi due).

La successione di Fibonacci è una successione ricorsiva lineare, definita nel modo seguente:

Ogni termine è quindi somma dei due termini che lo precedono: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,…

Partendo dall’osservazione e dallo studio di alcune spirali che si possono trovare in natura quali la disposizione dei petali di una rosa, la forma che caratterizza alcune conchiglie, il volo del falco pellegrino (e insieme a questi si potrebbero fare innumerevoli altri esempi) ci si accorge che hanno una proprietà che li accomuna alla successione di Fibonacci: si nasconde sempre lo stesso numero irrazionale comunemente indicato con la lettera greca φ, al quale tende il rapporto di termini successivi della successione di Fibonacci al tendere di n a infinito.

Il numero φ, detto numero aureo, è medio proporzionale tra l’intero segmento e la parte restante: una proporzione scoperta dai pitagorici e definita da Euclide nel suo scritto gli Elementi.

Una spirale logaritmica in cui il rapporto costante tra i raggi consecutivi è pari a φ si dice aurea; il rapporto fra un numero della successione di Fibonacci e il suo precedente è, al limite per n che tende ad infinito pari a φ.

La spirale di Fibonacci approssima molto bene la spirale aurea, tanto che a occhio nudo non si nota alcuna differenza tra le due. Il nome Spirale di Fibonacci è dovuto al fatto che le dimensioni dei lati dei quadrati con i quali si forma poi la spirale sono i termini della successione di Fibonacci (cliccare sui pulsanti frecce per vedere la costruzione passo passo o sul pulsante play definendo il tempo in secondi). 

Il rapporto aureo è quindi un anello importante di congiunzione, un punto d’incontro, tra la natura e la matematica.

La spirale logaritmica in natura

Come abbiamo detto, le spirali auree e la successione di Fibonacci si riscontrano in un’enorme varietà di fenomeni naturali.

“La matematica si può considerare come ciò che unisce e si interpone fra l’Uomo e la Natura, fra il mondo esterno e quello interno, fra il pensiero e la percezione”

F. W. August Fröbel

Galileo Galilei nella sua opera “Il Saggiatore” scriveva: «La filosofia è scritta in questo grandissimo libro che continuamente ci sta aperto innanzi agli occhi (io dico l’universo), ma non si può intendere se prima non s’impara ad intender la lingua, e conoscere i caratteri, nei quali è scritto. Egli è scritto in lingua matematica, e i caratteri son triangoli, cerchi, ed altre figure geometriche, senza i quali mezzi è impossibile a intenderne umanamente parola; senza questi è un aggirarsi veramente per un oscuro labirinto».

La matematica è il linguaggio della natura. La natura è armonica e simmetrica in ogni molti suoi aspetti, per comprenderla appieno l’uomo ha bisogno di strumenti adatti e lo “strumento” per eccellenza è la matematica.

La posizione delle foglie e la disposizione dei petali e dei semi di alcune specie seguono la forma della spirale logaritmica. La fillotassi, ovvero lo studio della disposizione dei diversi elementi nelle piante, spiega che la crescita di rami, foglie, semi e squame avviene in modo da essere ottimale e meno dispendiosa possibile: lo scopo è ridurre lo spreco di spazio. Nel 1907 G. van Iterson ha dimostrato che una serie di punti con distanza dal centro in progressione geometrica, disposti secondo un angolo di accrescimento di circa 137,5°, la sezione aurea dell’angolo di giro, viene vista come una coppia di famiglie di spirali (spirali vegetative), le une orarie e le altre antiorarie, in quantità̀ pari a due numeri di Fibonacci consecutivi. Per capire, variando lo slider n vengono rappresentati alcuni punti di due sole spirali con angolo di accrescimento di 137,5° in senso orario: 

Spirale nel mondo vegetale 

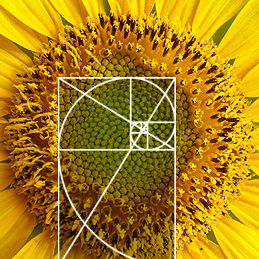I fiori di girasole sono un esempio significativo poiché disposti secondo due gruppi di spirali logaritmiche. Gli elementi di infiorescenza del fiore crescono in modo da occupare nel modo più efficiente possibile lo spazio circolare al centro del fiore. Il numero delle spirali dipende dalle dimensioni del fiore, ma in genere sono 55 disposte in un senso e 34 nel senso opposto. Anche nella pigna le squame sono disposte secondo spirali auree e allo stesso modo alcuni cactus e alcune piante rampicanti. Ma di esempi se ne potrebbero fare tantissimi, come l’ananas, il cavolfiore, la disposizione dei petali delle rose e la disposizione dei soffioni del cosiddetto “dente di leone”.

Spirale nel mondo animale

Come tra i vegetali, anche nel mondo degli animali molti fenomeni di accrescimento richiedono le proprietà̀ dell’omogeneità̀ e dell’autosomiglianza data dalla crescita logaritmica; infatti la struttura dell’animale, ingrandita o rimpicciolita, deve conservare sempre lo stesso aspetto. Per questo la spirale mirabile, detta appunto spirale “di crescita”, si può ritrovare ad esempio nelle conchiglie dei cefalopodi (phylum dei molluschi): i nautili, da miliardi di anni negli oceani, crescono secondo una spirale logaritmica mentre il crostaceo telescoptum (phylum: artropodi), ne segue una forma tridimensionale. La spirale di crescita si può ritrovare facilmente nelle conchiglie dei gasteropodi (phylum dei molluschi): lumache, chiocciole e trattole di mare, presentano coloratissime conchiglie a forma di spirali meravigliose. Anche alcuni fossili, come i foraminiferi o le ammoniti, possiedono questa forma.

Tutte queste strutture crescono secondo una crescita per addizione (accumulazione interna) e una crescita isometrica (un semplice ingrandimento), questo perché le conchiglie, che variano la propria forma in base logaritmica, sono adatte a contenere un organismo che cambia le proprie dimensioni ma non la propria forma, quindi una nuova sezione della conchiglia si forma quando l'organismo è cresciuto di una determinata percentuale costante rispetto allo stadio precedente.

Curiosamente anche gli insetti (phylum degli artropodi) hanno a che fare con la spirale logaritmica: perché́ gli insetti vanno a sbattere contro la griglia elettrificata delle lampade fulminanti? Sorprendentemente perché́ seguono una spirale logaritmica come traiettoria! La maggior parte degli insetti, infatti, si “orienta” nello spazio in base alla posizione del sole (o della luna), mantenendo un angolo fisso rispetto ai raggi di luce: la velocità del moto dell’insetto dipende da tale angolo. Per questo, essendo il sole un riferimento decisamente lontano, essi negli spazi aperti si muovono liberamente secondo traiettorie rettilinee. Tuttavia nel momento in cui l’insetto assume come riferimento la luce della lampada, molto vicina, seguendo un angolo costante piccolo (secondo una spirale equiangolare) si avvicina sempre di più̀ all’oggetto elettrizzato e entra in contatto con la lampada.

Un altro animale che sfrutta le proprietà della spirale è il falco pellegrino, uno degli uccelli più veloci al mondo (negli attacchi può raggiungere la velocità di 300 Km/h) e uno dei predatori più temibili a causa della sua vista acuta e della sua abilità di volo. Il biologo Vance A. Tuker si chiese come mai il falco, nel piombare su una preda, non scegliesse una traiettoria rettilinea, più breve e più veloce. Così arrivò a calcolare che il percorso seguito dal rapace è proprio una spirale aurea. Dal punto di vista pratico questo accade perché il falco, avendo gli occhi laterali, per vedere precisamente la preda dovrebbe ruotare la testa e perdere aerodinamicità̀. Invece percorrendo una spirale meravigliosa, il cacciatore non perde di vista la preda e ottimizza al meglio la velocità.

Si osservi che per ogni punto sulla spirale logaritmica è costante l’angolo tra la tangente alla curva in quel punto ed il raggio vettore. 

La spirale logaritmica e la sezione aurea nell’arte

Numerosi artisti nel corso della storia hanno utilizzato nelle loro opere il rettangolo aureo, la cui base è la sezione aurea dell’altezza, e le forme a spirale ricavate da costruzioni geometriche da esso derivanti. Esse infatti appaiono già nelle pitture e nelle incisioni rupestri preistoriche, ne sono esempi quella ritrovata nella grotta di Djerat presso Tassili-n Ajjer risalente al 6000 a.C., i motivi spiralici ad «­S» nel mosaico dei Disegni di Nazca oltre al capitello ionico dell'Eretteo e in opere architettoniche la facciata del Partenone di Atene.

Altri esempi si trovano nel Palazzo dell’ONU di New York e in pittura nelle opere di Vincent Van Gogh "Notte stellata" e "Autoritratto", nella "Gioconda" di Da Vinci oltre che nei suoi studi di anatomia tra cui troviamo il celebre "Uomo Vitruviano".

Le motivazioni dell’integrazione della spirale logaritmica nell’arte variano da semplice e puro scopo estetico come nell’art nouveau, di cui Parigi fu capitale indiscussa, all’espressione dell’equilibrio nello squilibrio e contemporaneamente della permanenza dell’essenza attraverso il cambiamento, poiché la spirale possiede la caratteristica di mantenere la sua forma nella sua crescita asimmetrica.

Sezione aurea e corpo umano

Leonardo nel disegno "Le proporzioni umane secondo Vitruvio" scrisse: “Vetruvio architetto scrisse nella sua opera d’architettura che lle misure dell’homo sono della natura disstribuite in quessto modo. Cioè, che 4 diti fa un palmo e 4 palmi fa un piè; 6 palmi fa un cubito, 4 cubiti fa un homo, e 4 cubiti fa un passo, e 24 palmi fa un homo; e cqueste misura son nè sua edifizi. Se ttu apri tanto le gambe che ttu chali da chapo 1/14 di tua alteza, e apri e alza tanto li bracci che colli lunghi diti tu tochi la linia della sommità del chapo, sappi che ’l cientro delle stremita delle aperte membra fia il bellicho. E llo spatio che ssi truova infra lle gambe fia triangolo equilatero”.

Con queste parole Leonardo da Vinci apre la descrizione dell’Uomo vitruviano, nelle cinque righe che si trovano nella parte alta del foglio conservato alle Gallerie dell’Accademia di Venezia in cui è rappresentato un corpo umano inscritto in un cerchio e in un quadrato; nel quadrato, l’altezza dell‘uomo (AB) è pari alla distanza (BC) tra le estremità delle mani con le braccia distese. La retta X-Y passante per l’ombelico divide i lati AB e CD in due parti in rapporto aureo tra loro. Lo stesso ombelico è anche il centro del cerchio che inscrive la persona umana con le braccia e gambe aperte. La posizione corrispondente all’ombelico è infatti ritenuta il baricentro del corpo umano.

Vincent Van Gogh e il rapporto con la spirale

Questo particolare quadro di Van Gogh è stato realizzato nello studio “improvvisato” che l’artista aveva avuto in concessione al pianterreno del manicomio di Saint-Paul-de Mausole dallo stesso staff della struttura. Con questo cielo stellato Van Gogh dà vita ad una visione completamente nuova della notte. La luna è stilizzata e diversa da come appare in realtà, inoltre è importante notare il campanile della chiesa, che è tipico dell’Olanda, nazione natale dell’artista; questi particolari lasciano intuire che, diversamente da molte altre delle opere di Van Gogh, Notte Stellata fu dipinta a memoria e non en plein air come egli era solito fare probabilmente introducendo pesanti modifiche al paesaggio originale. Questo può forse spiegare, in parte, perché l’impatto emotivo dell’opera sia assai più forte che in altre opere di van Gogh dello stesso periodo.

Tale impatto emotivo è dovuto per la maggior parte alla straordinaria rappresentazione del cielo, ed è qui che entra in gioco la spirale logaritmica che va a conferire un accezione sinuosa percepibile in tutta la scena dando l’impressione che l’intero cosmo sia vivo e in movimento; secondo alcuni studiosi di astronomia questi “turbini” nell’aria non sono solamente stratagemmi per suscitare emozioni nell’osservatore, ma la rappresentazione del vento, o, per essere più precisi, il Maestrale che soffiava spesso in Provenza, proprio dove si trovava Vincent.

La Mole Antonelliana

Dal 2001 la Mole Antonelliana ospita l’opera d’arte concettuale di Mario Merz il "Volo dei numeri": i primi termini della successione di Fibonacci, riprodotti con neon rosso, sono disposti verticalmente in ordine crescente dal basso verso l'alto. Con questa istallazione l’artista, esponente di spicco del movimento Arte povera e da sempre attratto da questi numeri, ha voluto rappresentare l'esplosivo processo organico di crescita insito in moltissimi fenomeni naturali.