Le successioni

Una successione numerica è una funzione che associa ad ogni numero naturale n uno ed un solo numero reale a_n.  Quindi essa ha come dominio l’insieme dei numeri naturali N, privato eventualmente di qualche elemento e come codominio l’insieme dei numeri reali R o un suo sottoinsieme.

I termini di una successione vengono indicati con i simboli a₀, a₁, a₂, … , a_n, …, dove n indica la variabile indipendente e prende il nome di indice della successione ed a_n, l’n-esimo termine della successione, è la variabile dipendente detto termine generale della successione.

Il grafico di una successione è un insieme di punti (n, a_n) “isolati”, che formano un insieme discreto, a differenza del grafico di una qualsiasi funzione definita da R a R, che è l'insieme di punti (x, f(x)) “non isolati” che formano un insieme continuo.

Una successione può essere rappresentata in diversi modi:

1. RAPPRESENTAZIONE PER ENUMERAZIONE O ELENCAZIONE

Consiste nell’elencare i suoi primi termini, seguiti da puntini di sospensione. Il numero dei termini deve essere sufficiente perché si possa dedurre quale sia "la regola" per determinare i successivi termini della successione.

Esempio                           0, 1, 4, 7, 10, 13, 16, 19, …       

Il termine successivo si ottiene sommando 3 al precedente.

2. RAPPRESENTAZIONE RICORSIVA

Le successioni definite per ricorrenza sono tali che ogni termine della successione, escluso il primo che viene definito direttamente, dipende dal termine precedente. Cioè, dopo aver definito il primo elemento della successione, si stabilisce una regola che permette di calcolare il successivo.

 Esempio

Determinare i primi quattro termini della successione definita per ricorsione:

A partire dal primo termine si determinano quelli successivi:

 

3. RAPPRESENTAZIONE MEDIANTE ESPRESSIONE ANALITICA

Consiste nello scrivere esplicitamente la relazione che lega l’indice n ed il termine a_n.

Esempio

Per scrivere i primi termini della successione basta determinare le immagini della funzione sostituendo alla lettera n, nell’espressione a_n i valori 1, 2, 3, 4, …, si ha quindi:

Una successione si dice:

Progressione aritmetica

Una progressione aritmetica è una successione di numeri reali, tali che la differenza tra un elemento, a partire dal secondo, ed il suo precedente è costante.

La successione numerica:

a₁, a₂, a₃, a₄, a₅...a_n

è una progressione aritmetica se la differenza fra qualsiasi termine della successione (escluso il primo) ed il suo precedente è costante, cioè: 

 

d è detta ragione della progressione.

Quindi si ha:

in generale, il termine n-esimo è uguale a:

 

che rappresenta la relazione fondamentale fra il termine n-esimo della progressione aritmetica, il primo termine e la ragione costante d.

Esempio

Determinare il decimo termine della progressione aritmetica che ha il primo termine a₁=3 e la ragione d = 2.

Applicando la formula si ha:

 

Relazione tra due termini di una progressione aritmetica

Se a_r ed a_s sono due termini di una progressione aritmetica, è possibile ricavare il termine s-esimo, conoscendo l’r-esimo e la ragione d: da a_s= a₁+(s-1)d e a_r= a₁+(r-1)d, sottraendo membro a membro si ottiene a_s- a_r=(s-1-r+1)d da cui

Si possono ovviamente ricavare le relazioni inverse che permettono di determinare un’incognita a piacere conoscendo le altre due. 

Inserimento di k medi in progressione aritmetica tra due elementi.

Considerati due numeri reali α, β (α < β), è possibile inserire, tra questi, k elementi x₁, x₂, x₃, x₄, x₅...x_K  in progressione aritmetica.

Ciò che si vuole fare è scrivere gli elementi

a₁ = α, a₂ = x₁, a₃ = x₂, a_k+1 = x_k, a_k+2 = β

della successione, cioè:

a_k+2= a₁ + (k + 2−1)d

ovvero

β = α + (k + 1)d

da cui si ottiene la ragione d:

ne segue che

Si noti che, per k = 1, si ottiene l'inserimento del medio x tra i numeri α e β che rappresenta proprio la loro media aritmetica.

Esempio:

Inserire 4 elementi in progressione aritmetica tra i numeri −2 e 1.

Si calcola la ragione d: 

I numeri cercati sono quindi:

Somma di n termini consecutivi di una progressione aritmetica

Si racconta che il maestro delle elementari di F. Gauss, propose questo problema sperando di impegnare i suoi studenti per almeno 1 ora: “Sommare i primi 100 numeri naturali”. Quello che chiedeva il maestro era determinare il risultato di:

Guass risolse il problema in molto meno di 1 ora, senza sbagli e scoprendo un modo per eseguire la somma non solo dei primi 100 numeri naturali, ma anche dei primi 1000 o 10000 in poco tempo. Ecco come fece. Dispose i numeri da 1 a 100 in ordine crescente e poi li riscrisse allineati in colonna ordinandoli in modo decrescente.  Infine eseguì la somma in colonna scoprendo che otteneva 101 ogni volta, ossia 100 volte.

Il risultato della somma dei primi 100 numeri risultava essere quindi:

 

È facile ora estendere il ragionamento di Gauss ad una successione aritmetica qualunque di cui si voglia determinare la somma di n termini consecutivi di cui sia noto il primo e l’ultimo, ottenendo la formula generale:

Esempio

Determinare la somma dei primi 20 termini della progressione aritmetica che ha il primo termine a₁=1 e la ragione d=2 (somma dei numeri dispari minori di 40).

Poiché n=20, a₁=1 , a₁₀=39, la somma dei primi 20 numeri è:

Progressione geometrica

Una progressione geometrica è una successione di numeri reali, tali che il rapporto fra un qualsiasi termine, a partire dal secondo, della successione ed il suo precedente è costante.

La successione numerica:

a₁, a₂, a₃, a₄, a₅...a_n

rappresenta una progressione geometrica se:

q è detta ragione della progressione geometrica.

Quindi si ha:

in generale, il termine n-esimo è uguale a:

che rappresenta la relazione fondamentale fra il termine n-esimo della progressione geometrica, il primo termine e la ragione costante q.

Relazione tra i termini di una progressione geometrica 

Se a_r ed a_s sono due termini di una progressione geometrica, è possibile ricavare il termine s-esimo, conoscendo l’r-esimo e la ragione q: da a_s=a₁q^s-1 e a_r=a₁q^r-1 dividendo membro a membro, semplificando e ricavando a_s si ottiene

Si possono quindi ricavare le relazioni inverse che permettono di determinare un’incognita a piacere conoscendo le altre due.

Inserimento di “m” medi geometrici fra due estremi

Considerati due numeri reali positivi a e b, è possibile inserire tra questi m numeri positivi, in modo da ottenere i primi m+2 termini di una progressione geometrica.

Innanzitutto bisogna determinare la ragione q della progressione geometrica, sfruttando la relazione inversa del termine generale

con a_n=b, a₁=a e n=m+2, ossia b=aq^m+1, da cui

Quindi 

 

Un esempio importante consiste nell’inserire un medio geometrico fra due numeri a e b.

Se m=1, la ragione è data da   

e quindi il numero medio m, da inserire tra a e b è dato dalla seguente formula:

quindi è la media geometrica dei due numeri a e b.

 Il medio geometrico fra due estremi corrisponde al medio proporzionale di una proporzione continua del tipo: 

Somma di n termini consecutivi di una progressione geometrica

Per il calcolo della somma dei primi n termini di una progressione geometrica, si considera la somma S_n di n termini

moltiplicando entrambi i membri per q si ottiene

e sottraendo membro a membro le due uguaglianze e semplificando si ottiene:

da cui:

Esempio

Determinare la somma delle prime 10 potenze di 2 con esponente diverso da zero.

I numeri di cui si vuole calcolare la somma sono i primi 10 termini della progressione geometrica di ragione 2 e primo termine 2:

2, 4, 8, 16, 32, 64, 128, 256, 512, 1024.

 Applicando la formula si ha:

Dalla progressione geometrica alla funzione esponenziale

Come tutte le successioni, una progressione geometrica rappresentata dal termine generale

è definita nell’insieme dei numeri  naturali.

Se si considera come insieme di definizione non più l’insieme discreto N, ma l’insieme continuo R, se q è un numero reale positivo (si ricorda che una potenza a esponente reale è definita solo per basi positive), si ottiene la funzione definita in R

detta funzione esponenziale di base q.

Posto a₀=1  si ottiene

Si riportano in figura i grafici della funzione f(x)=2^x con x intero relativo, nel primo grafico e con x reale nel secondo.

La funzione esponenziale

Si chiama funzione esponenziale ogni funzione in cui la variabile indipendente compare all'esponente di potenze con base positiva e diversa da 1.

Si osservi che per a=1 l'equazione rappresenterebbe la funzione costante y=1.

Esempi di funzioni esponenziali sono

 

Costruzione del grafico della funzione esponenziale con GEOGEBRA

Per creare il grafico della generica funzione esponenziale y=a^x sono stati seguiti i seguenti passaggi:

-        creare uno slider attribuendogli il nome a                    

-        indicare l’intervallo di a (positivo, ad esempio da 0.1 a 10, con un incremento di 0.1)

-        scrivere l'equazione y=a^x della funzione esponenziale nella barra di inserimento      

Variando il valore di a muovendo il punto sullo slider si ottengono i diversi grafici della funzione.

 

UNA BASE “SPECIALE”

Una base speciale della funzione esponenziale è un numero irrazionale che viene indicato con la lettera e, che vale e=2,7182818.. troncato alle prime sette cifre decimali, detto numero di Eulero in onore del matematico che contribuì alla sua scoperta. Di questo numero si parlerà nei capitoli sui numeri irrazionali e sulla storia del logaritmo.

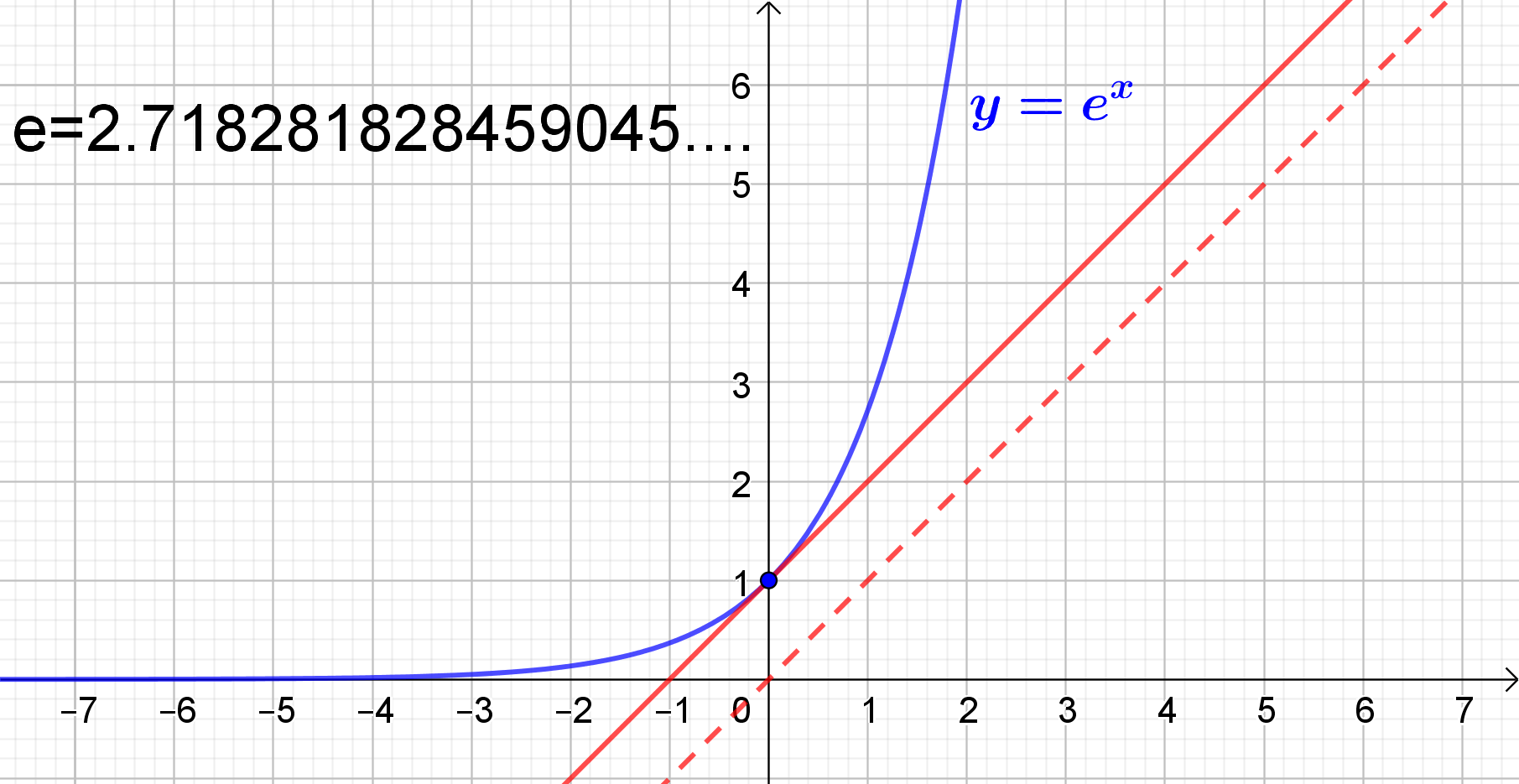
La funzione y= e^x ha un'importante proprietà: la retta tangente alla curva nel punto (0,1) è parallela alla bisettrice del I e III quadrante.

OSSERVAZIONE

Se le funzioni esponenziali hanno base reciproca, allora i loro grafici risultano simmetrici rispetto all’asse y

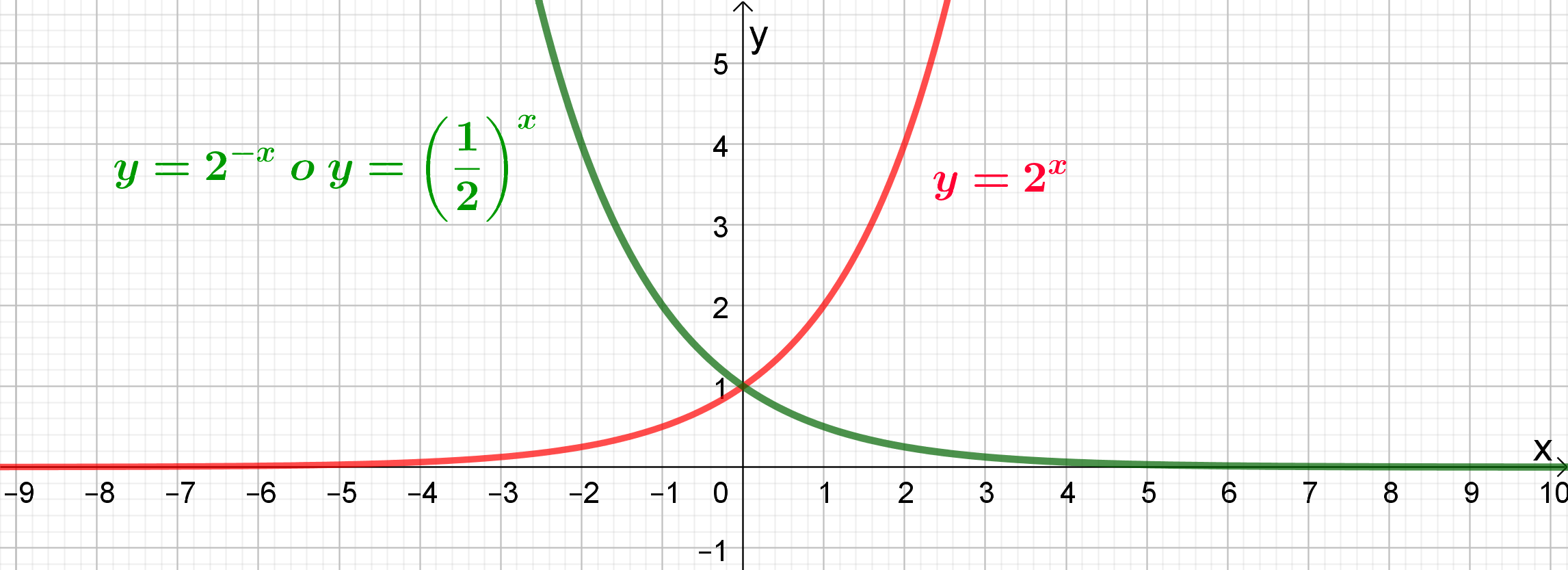
Le funzioni esponenziali sono utilizzate come modelli per descrivere fenomeni reali di crescita o di decrescita, alcuni dei quali saranno descritti nei capitoli successivi.